Wie kann die Besonderheit der Fünf wirklich nutzbar gemacht werden?

In den gängigen Rechenbüchern finde ich außer einigen Beispielen zum strukturierten Zählen mit „5 plus x“ und zum Zerlegen der Zahlen 6 bis 9 nichts, was die Kinder beim Erobern der Zahlenwelt näher an die nächste wichtige Hürde bringt: Das verständnisbasierte Überschreiten der Zehnergrenze beim Addieren.
Im Zahlenbuch, das meiner Meinung nach das beste der zur Zeit verfügbaren Rechenbücher ist, wird immerhin auf einer Seite die Tatsache behandelt, dass zwei Fünfer immer Zehn ergeben.
Da gibt es den Vers von den zehn kleinen Zappelmännern und eine Reihe von Bildern mit jeweils zwei Fünfermengen: eine Eierschachtel, zwei Fünfer-Würfelbilder, zwei 5-Euro-Scheine, zwei Fußabdrücke usw.

Aber ist das wirklich genug, um so pathetisch von der „Kraft der Fünf“ zu sprechen? Wenn’s da nicht mehr gibt, ist das in meinen Augen sehr übertrieben.

Die Fünf kann uns viel mehr bieten, nämlich das handlungsorientierte und verständnisbasierte Herangehen an zwei der wichtigsten Schlüsselfähigkeiten des flinken und sicheren Rechnens:
An das passgenaue Zerlegen und das gezielte Auffüllen zur nächsten Stellenwertgrenze.

Hier betritt der Fünferräuber die Bühne

Mit Kindern rechnen zu lernen, kann eine phantastische Sache sein. Dafür musst du dich allerdings immer wieder darauf einlassen, in die Erlebniswelt der Kinder einzutauchen. Das habe ich schon in einigen Beiträgen erwähnt, aber der Fünferräuber ist eine ganz besondere Nummer.

Mit Freude rechnen heißt natürlich auch: besser rechnen!

Unsere Schulanfänger haben zu Märchenfiguren noch eine sehr enge Beziehung. Wenn nun der Räuber im Unterricht auftaucht, so ist das eine Bezugsperson, die die Phantasie der Kinder anregt und das Abstrakte sehr konkret werden lässt.
Die Voraussetzung dafür ist allerdings, dass der Räuber nicht nur zur Gaudi da ist, sondern dass er den Kindern wirklich auch etwas abverlangt.
Ich halte wenig von Unterrichtsmaterial, bei dem am Seitenrand oder auch mittendrin irgendeine „lustige“ Figur sitzt, die vielleicht in den Augen der Schulbuchautoren motivierend wirkt, die aber keine andere Funktion hat, als Merksätze und Überschriften auf Schildern oder in Sprechblasen zu übermitteln.
Ich glaube nicht, dass der Rabe Trax, der Bär Bibu, ein Löwe oder ein Elefant, die unsere kleinen Rechner durch das Buch „begleiten“, wirklich für dauerhafte Rechenlust und Denkfreude sorgen können. Und mit dem richtigen Rechnen haben sie außerdem gar nichts zu tun, denn die Überschriften und Merksätze würden ihre Bedeutung auch ohne die Garnierung mit den Figuren übermitteln können.

Der erste Auftritt unseres Räubers

Dafür brauchst du eine Räuber-Handpuppe. Je nach deiner Lust an Drama und Schauspiel kannst du diese Puppe nun etwas mehr oder weniger theatralisch auftreten lassen.

Bei mir ist der Räuber unter einem Stapel Papier – zunächst noch verdeckt – gelegen und hat durch lautes Schnarchen auf sich aufmerksam gemacht. Er wurde dann schließlich unter dem Papierstapel „gefunden“, ist aufgewacht und hat gleich laut nach Essen geschrien, und zwar nach Fünfern, die mag er so gern und er hat gehört, dass es in der Schule ganz viele Fünfer gibt, deshalb ist er hier.

Ich rieche, rieche Fünfer!

Das wird sein „Schlachtruf“, mit dem er uns alle ordentlich auf Trab hält. Er legt bei seinem ersten Auftritt auch gleich damit los und ich habe die Tafel schon vorbereitet. Darauf stehen nämlich 6er, 8er, 7er und 9er. Und die Kinder wissen auch gleich, wie wir an Fünfer für den Räuber kommen. Wir zerlegen die Zahlen und schon kann er die Tafel leerfressen. Dass die Fünfer nach dem ganzen Geschmatze immer noch da sind, stört die Kinder nicht. Das ist nur in unserem Erwachsenenhirn von Belang.
Über den Umgang mit dem Fünferräuber findest du noch weitere ausführliche Informationen in meinem Buch „So lernen alle Kinder rechnen“.

Was bringt der Räuber mathematisch?

In einem allerersten Schritt beschäftigen wir uns mit der Zerlegung der Zahlen 6 bis 9, das ist nichts anderes als in den Rechenbüchern, aber es ist nur das Sprungbrett zu weit anspruchsvolleren Aufgaben.

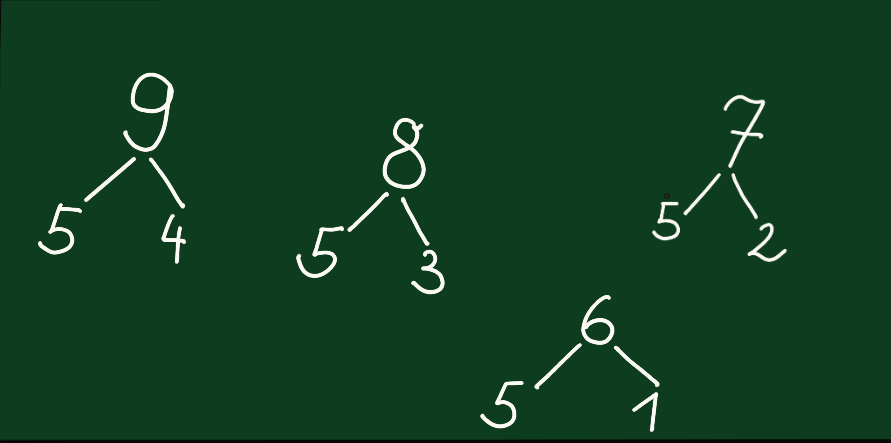
Bei diesem allerersten Schritt wird dann die Zerlegung in 5 + n auch noch handelnd ausgeführt. Die Geschichte dazu: Der Räuber isst immer Teller mit fünf Knödeln. Die richten wir ihm her. Unsere oben angeschrieben Zahlenzerlegungen sehen nun so aus:

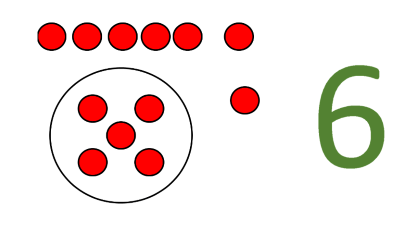
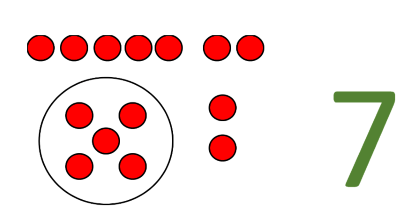
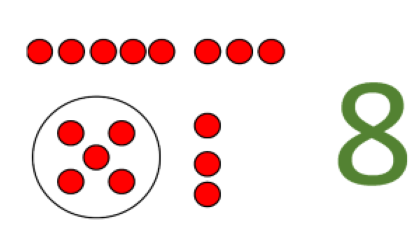
In einem nächsten Schritt wird gezielt am Zerlegen und Auffüllen gearbeitet und zwar nur mit dem Ziel, möglichst viele Fünfer für den Räuber zu bekommen.

Das Besondere beim Zerlegen der Fünf:
Eine Menge aus 5 Elementen ist die kleinste Menge, die wir – wenn sie ungeordnet ist – nicht mehr simultan mit einem Blick erfassen können.
Das heißt, wir müssen diese Menge optisch strukturieren in zwei Teilmengen. Dafür wiederum gibt es nur zwei Möglichkeiten:

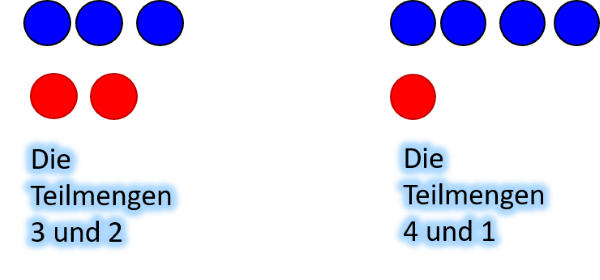
Das heißt, du kannst diese wichtige Schlüsselfähigkeit des passgenauen Zerlegens in einem kleinen Zahlenraum üben und die Teilmengen wiederum sind so klein, dass sie noch simultan erfassbar und damit auch simultan vorstellbar sind.

Und dann hast du diese Menge auch noch repräsentiert durch die Finger einer Hand. Du kannst diese Zerlegungen also auch durch das entsprechende Spreizen der Finger zeigen.
Wer jetzt sagt: Igitt, mit den Fingern rechnen, der übersieht etwas. Wir RECHNEN nicht, wir ZEIGEN Mengen, das ist eine ganz andere Baustelle und hat nichts zu tun mit dem mechanischen Abzählen von Rechenergebnissen an den Fingern.

Warum heißt es, wir zerlegen passgenau?

Jetzt kommt wieder unser Räuber ins Spiel: Wir füllen Knödelteller, und um immer genau fünf zu bekommen, müssen wir manchmal auch zwei Teilmengen zu einer Fünf zusammenlegen. Damit wir wissen, welche Teilmengen zhsammenpassen, müssen wir natürlich die Zerlegungen parat haben. Nun wird es durchaus etwas schwierig und die Kinder müssen den Überblick behalten über eine ganze Menge von Zahlen.

Das fällt übrigens den Kindern leichter als den Erwachsenen. In Lehrerfortbildungen kommt an dieser Stelle oft Unsicherheit auf, manchmal sogar Unmut, denn hier verlassen wir die Schulbuchroutine und müssen auch als Erwachsene richtig mitdenken.

Das ist der nächste Schwierigkeitsgrad der Fünfer-Aufgaben:

Wie viele Fünfer sind in dieser Zahlenreihe versteckt?

So sieht die Lösung aus:

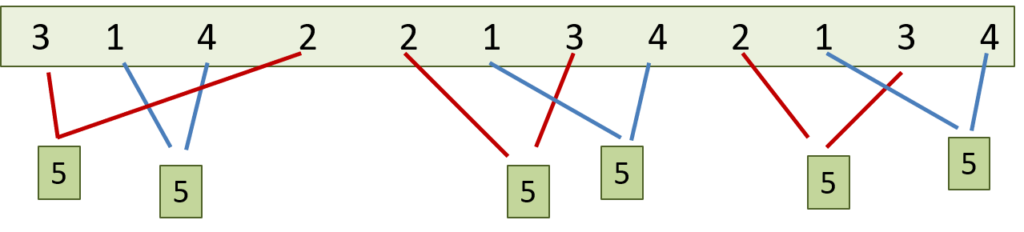
Und jetzt wird’s noch komplizierter:

Manche Zahlen – die roten – sind größer als 5, die müssen zerlegt werden in 5 + n, manche Zahlen – die gelben – sind kleiner als 5, die brauchen wir zum Zusammenstückeln.

So sieht hier die Lösung aus:

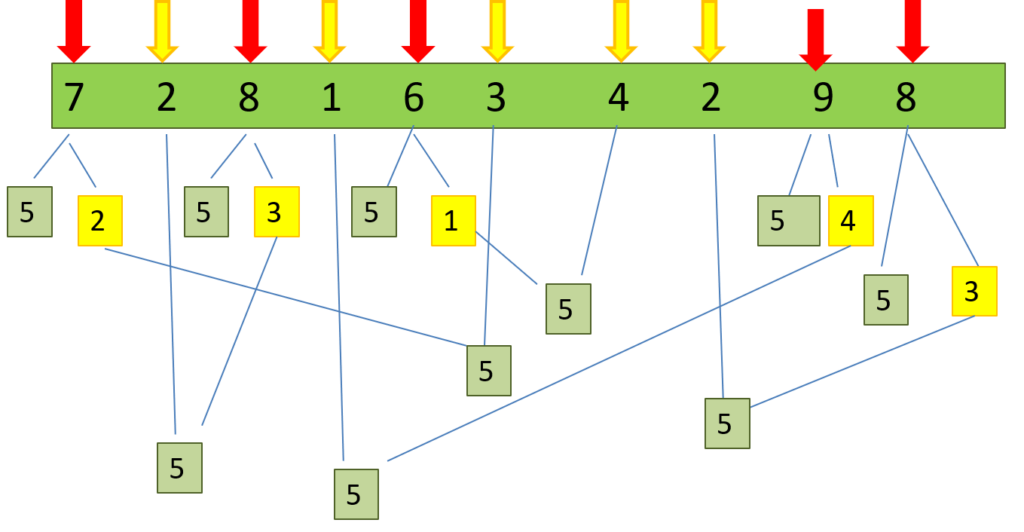
Und als Extra-Schmankerl für die Kinder kann nun noch die Gesamtzahl der einzelnen Knödel ermittelt werden.

Wir halten für jeden Fünfer – also für jeden gefüllten „Knödelteller“ eine Hand hoch. Da brauchen wir einige Kinder, die ihre Hände hochhalten:

Ein Lieblingsspruch des Räubers – mit dem er uns auch richtig auf die Nerven geht – ist: Eine Hand und noch ne Hand ist zehn!

Also legen die Kinder ihre Hände zusammen und wir sehen jetzt lauter Zehner:

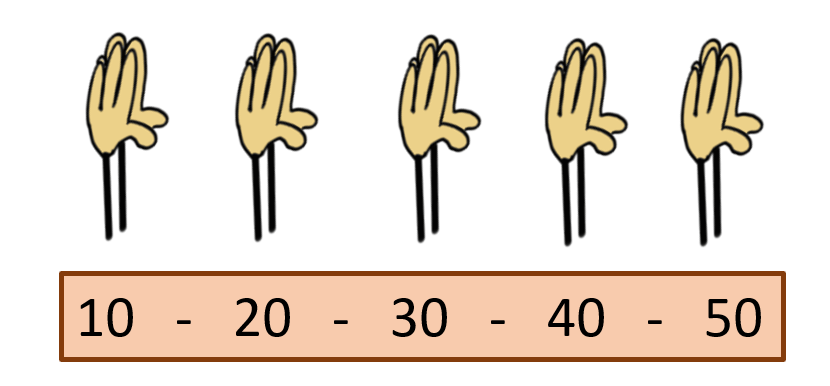
Du meinst, das sei zu schwierig? Da unterschätzt du die Denkfreude und Denkfähigkeit der Kinder. Genau das ist gerade herausfordernd genug, um sie anzuspornen und nicht so schwierig, dass es nicht zu bewältigen wäre. Und das Herauskommen und Hände hochhalten bringt Bewegung und Spielfreude in den Unterricht.
Das Bilden der Zehner aus den einzelnen Fünfern kann durch einen Helfer erfolgen, der langsam bei jedem Kind die beiden hochgestreckten Hände zusammenlegt, während die ganze Klasse mitzählt: „Zehn, zwanzig, dreißig …“

Jetzt geht’s erst richtig los: Der Fünferräuber rechnet!

Bis hierher gab es schon einiges zu denken, aber dabei bleiben wir nicht stehen. Der Räuber, der uns nun täglich in der Schule besucht, will rechnen und er hält sich für sehr schlau, sagt auch oft seinen Lieblingsspruch auf. Dann verdrehen wir die Augen, aber genau dieses Spiel mit dem „nervigen“ Räuber führt dazu, dass alle felsenfest in ihrem Gehirn verankern, dass eine Hand und noch ne Hand – also 5 + 5 – zehn sind.

Die Rechnungen mit den Knödeltellern des Räubers führen zu einem Zehnerübergang, bei dem aus zwei Fünfern der Zehner zusammengesetzt wird. Wir brauchen also genau das, was wir im Vorfeld beim Bilden von „Knödeltellern“ – also Fünfermengen – geübt haben.

Dieser Zehnerübergang mit der „Kraft der Fünf“ kann sehr gut zu Beginn des zweiten Trimesters – in Bayern also im Januar – eingeführt werden.

In vielen Klassen wird erst gegen Ende des ersten Schuljahres noch „schnell“ der Zehnerübergang durchgenommen, das ist viel zu spät.

Wenn du zuerst einmal nur bei den Plusrechnungen über den Zehner gehst, können die Kinder dieses Überschreiten der Zehnergrenze viel früher lernen und gründlicher üben, denn sie haben dann ja reichlich Zeit.

Und so rechnet der Räuber:

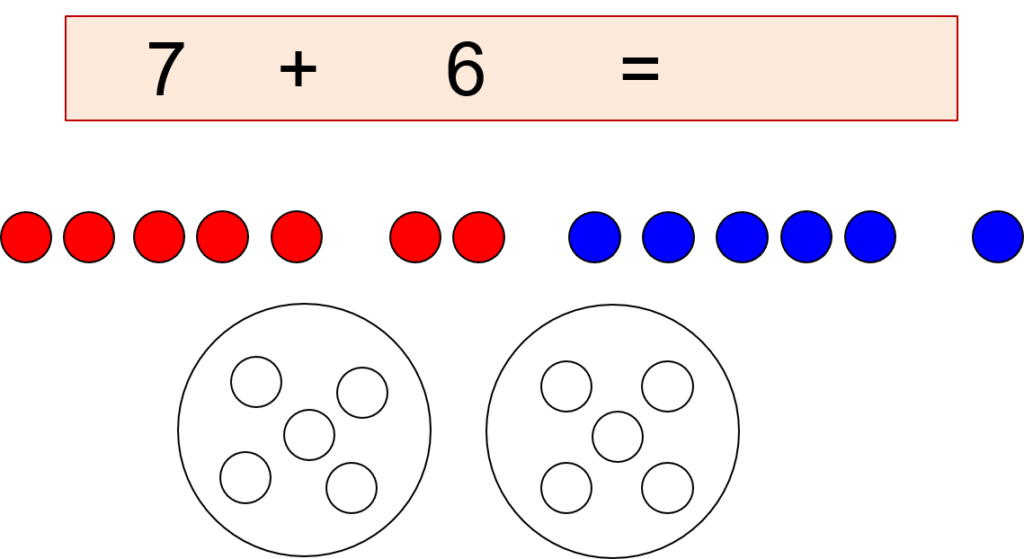
7 rote und 5 blaue Perlen stehen für den 1. und 2. Summanden.
Die beiden Knödelteller werden gefüllt, dann haben wir einen Zehner.

Erste Möglichkeit für eine Lösung:

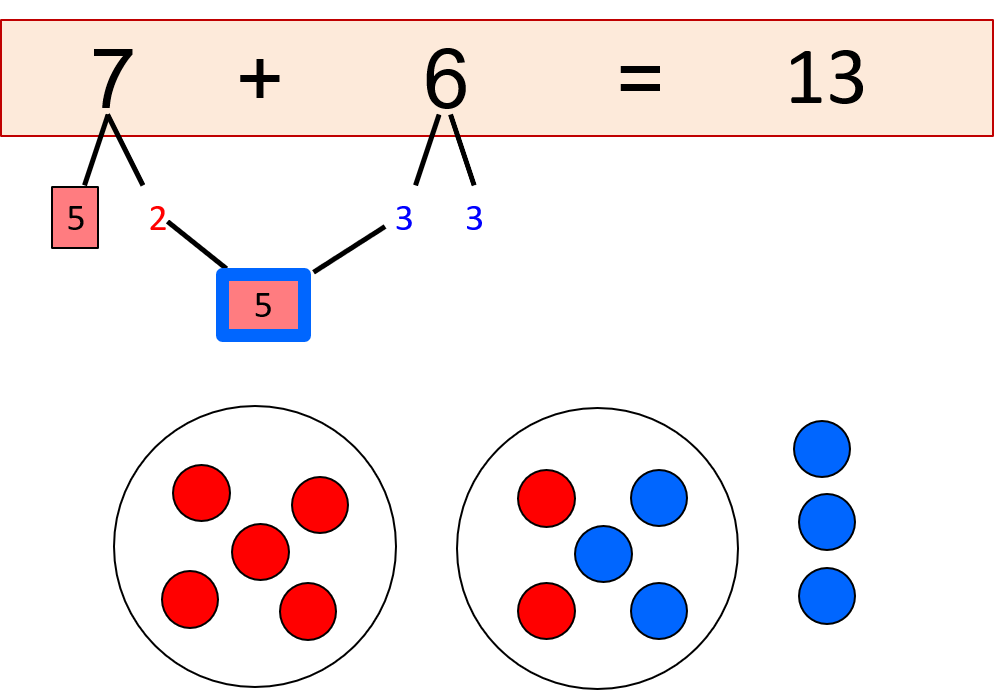
Die rote Sieben wird in 5 + 2 zerlegt und zu der roten Zwei kommt eine blaue Drei, die wir aus der Zerlegung 6 = 3 + 3 bekommen.
Die beiden Teller ergeben zehn und übrig bleiben 3 blaue Perlen – also Einer.

Zweite Möglichkeit für eine Lösung:

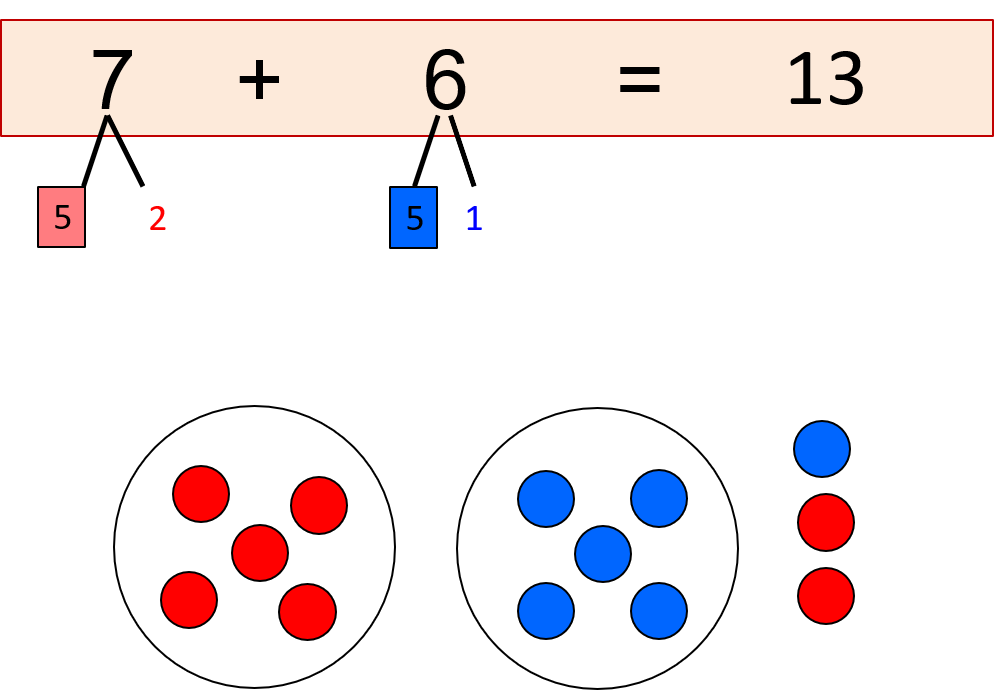
Es wird ein roter und ein blauer Knödelteller gebildet, als Einer bleiben 3 rote und eine blaue Perle übrig.

In diesen Aufgaben steckt jede Menge Denkarbeit und wenn du diese Rechnungen mit dem Fünferräuber vor den „eigentlichen“ Zehnerübergang schaltest, dann wirst du sehen:
Der Zehnerübergang fällt vom Baum wie eine reife Frucht!

Viele Tipps für das Rechnen mit dem Fünferräuber und Arbeitsblätter dazu findest du in meinem Buch:
So lernen alle Kinder rechnen und im Arbeitsblätterheft für die erste Klasse.