Minus ist nicht sehr beliebt

Während die Nicht-Denker bei Plusrechnungen in kleinen Zahlenräumen sich mit der Krücke des Abzählens an den Fingern zunächst einmal ganz gut durchschwindeln können, ist das Rückwärtszählen schon deutlich schwieriger.
Außerdem ist auch die Vorstellungskraft stärker gefordert, wenn es darum geht, dass etwas wegkommen soll. Und überhaupt ist es nicht so attraktiv, etwas herzugeben.

Gerade weil das Minusrechnen in jeder Hinsicht komplizierter ist als das Addieren sollte es erst eingeführt werden, wenn der Boden dafür gut vorbereitet ist.
Die gängige Rechenbuchpraxis, bereits sehr früh – deutlich vor Weihnachten – Gleichungen mit Plus und Minus anzubieten, halte ich für kontraproduktiv.

Da rechnen die Kinder im Zahlenraum bis zehn die immer gleichen Aufgaben, wissen einerseits gar nicht so genau, was sie da eigentlich tun und sind andererseits total gelangweilt, weil es eben nichts wirklich Herausforderndes zu handeln und zu denken gibt.

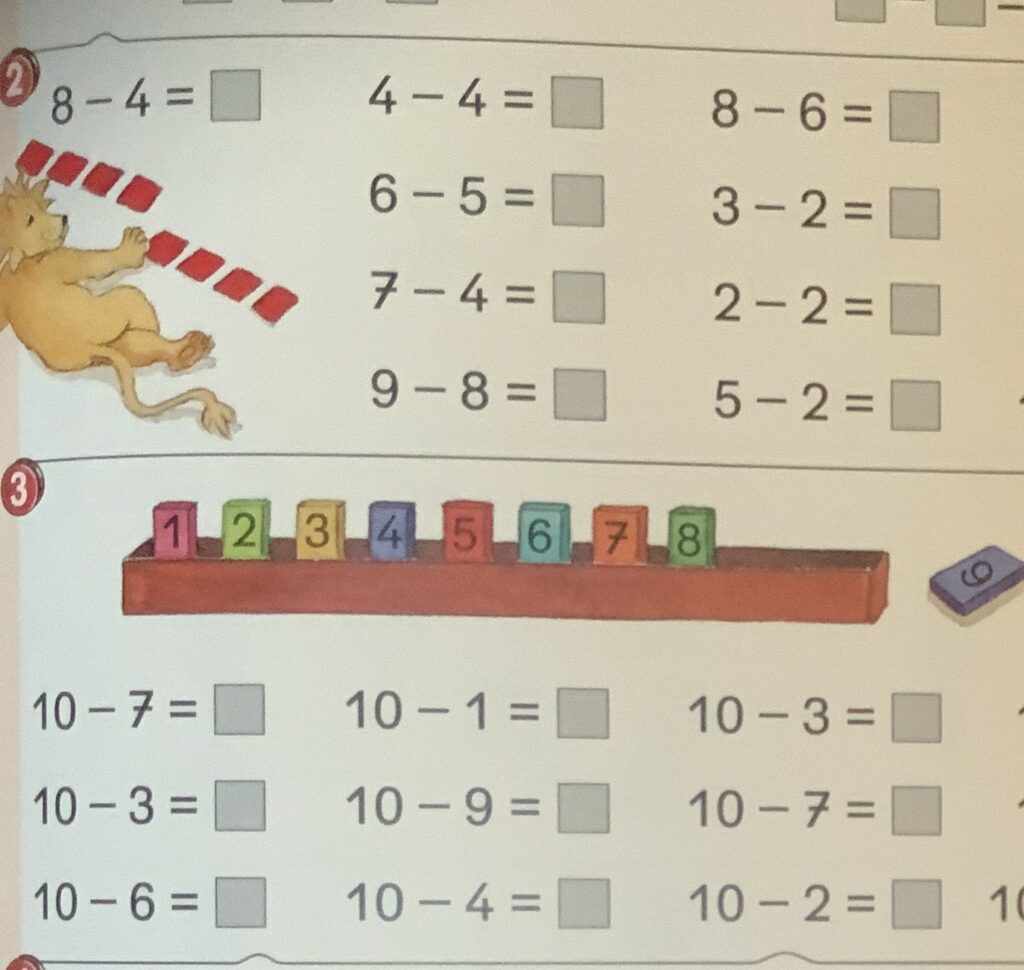
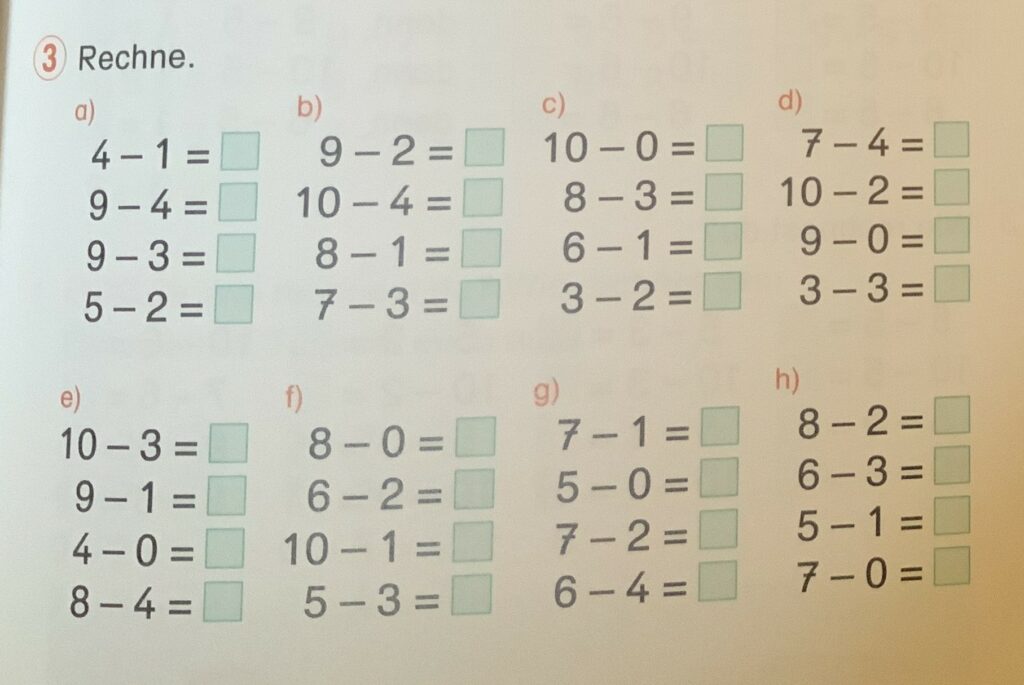
Die Bezüge zu Sachsituationen, die über Bilder hergestellt werden sollen, sind meiner Erfahrung nach nicht eindeutig genug. Sie müssten schon in der Realität mit echten Gegenständen nachgespielt werden, um wirklich jedem Kind eine Chance zu geben, den Sachverhalt zu begreifen. Das aber geschieht in der Schulwirklichkeit fast nie.

Der richtige Zeitpunkt

Ich habe die allerbesten Erfahrungen mit dieser zeitlichen Abfolge gemacht:
Erstes Trimester der ersten Klasse:
Vertraut werden mit dem ganzen Zwanzigerraum, Spiele und Ordnungsübungen vom zweiten Schultag an, Zahlenzerlegungen bis 10 handelnd erwerben und üben, Verdopplungen mit dem Spiegel, Zahlen schreiben und legen bis 20, Zehner und Einer mit Säckchen und Kugeln darstellen, keine Gleichungen, naive Notationen über Äste und Tabellen.

Zweites Trimester der ersten Klasse:
Einführen des Plus, kurze Phase der Additionen im Zehnerraum, Zehnerübergang mit der Fünfergliederung (Fünferräuber), Zehnerübergang mit der Zehnerliesel.

Und erst im dritten Trimester der ersten Klasse:

Einführen des Minus, Erforschen des Zusammenhangs von Plus und Minus, Tausch- und Umkehraufgaben,
nach kurzer Phase der Subtraktionen im Zehnerraum Minusrechnen mit Zehnerunterschreitung und dem Krokodil Schnappi.

Vorteile dieser späten Einführung des Minus

Die Kinder haben den Zahlenraum bis 20 auf unterschiedliche Weisen gründlich erforscht und haben durch das Spielen von Sachsituationen und durch das Ergänzen bei Ästeaufgaben mit dem mathematischen Prinzip des Minus implizite Erfahrungen gesammelt, auch wenn das nicht explizit so genannt wurde.
Sie haben durch die Arbeit mit dem Fünferräuber und durch die Zehnerüberschreitung bei den Additionen einen geschickten Umgang mit Zahlen und Mengen erworben, haben ihre Vorstellungskraft geschult und haben die Zahlzerlegungen bis zehn auswendig auf Lager, sodass sie bestens gerüstet sind.

Die Beziehung von Minus und Plus

Um das Minus nicht nur als bloßes Abstreichen oder Rückwärtsgehen darzustellen, sondern es von Anfang an in seiner Beziehung zu den Additionen zu sehen, die ja quasi seine Kehrseite sind, führe ich die Idee des Minus über das Mischen und Ent-Mischen von Farben ein.

Dazu brauchst du je eine Flasche rote und gelbe Farbe, Pinsel, Pappteller zum Farbenmischen und Blankobierdeckel. Bei den Farben musst du vorher eine Probemischung machen, denn nicht alle roten Farben lassen sich mit Gelb so mischen, dass wirklich ein schönes und deutliches Orange herauskommt. Ich habe mit Dispersionsfarben und auch mit Fingerfarben gute Erfahrungen gemacht , habe aber auch schon einmal daneben gegriffen – also: unbedingt vorher ausprobieren!

Blanko-Bierdeckel werden mit roter, gelber und der orangen Mischfarbe bemalt.

Auf die gefärbten Bierdeckel werden mit Edding Zahlen geschrieben und dann kann ein Zahlentripel gelegt werden:
Wenn ich die rote Fünf und die gelbe Drei zusammenmische, bekomme ich die orangefarbene Acht.
Oder andersherum: In der orangen Acht stecken die rote Fünf und die gelbe Drei.
Jetzt wird’s spannend: Beim Mischen entsteht eine neue Farbe. Kann ich das Ganze auch wieder rückwärts abwickeln?

Wie kann die orange Farbe wieder ent-mischt werden?

Du wirst dich jetzt vielleicht fragen, warum das wichtig sein soll. Das ist viel mehr als eine bloße Spielerei: Es geht um den Zusammenhang der beiden Grundrechenarten Plus und Minus. Es ist ja so, dass beim Addieren zwei Mengen zusammenkommen oder, wie ich kindgerecht immer sage:
Ein Haufen und noch ein Haufen ergeben zusammen einen größeren Haufen.

Mathematisch ausgedrückt zum Beispiel: 5 + 3 = 8

Bei dieser Rechnung st es so, dass in der Acht die Fünf und die Drei enthalten sind. Wenn ich aus der Acht eine der beiden Zahlen herausziehe, bleibt zwangsläufig die andere übrig.
Wird das nun mit den Farben Rot, Gelb und Orange verbunden, so haben die Kinder einen Trigger, der ihrem Hirn die genau richtige Vorstellung liefert.
Weil es aber nicht geht, aus den vermischten flüssigen Farben wieder eine Farbe zu extrahieren, nehme ich nun, nachdem das Prinzip des Mischens ja gemeinsam mit den Kindern erfahren wurde, zwei Folienstücke von Prospekthüllen, die es überall zu kaufen gibt, in den Farben Rot und Gelb. Das Rot ist zwar mehr ein Rosa, aber das spielt für die KInder keine Rolle, es wird einfach „zu Rot erklärt“, und schon kann’s losgehen.

In Folien-Farben ausgedrückt sieht das Ganze dann so aus:

Gelbe und „rote“ Folie werden auf einen weißen Hintergrund gelegt. Die rote Folie soll „5“ sein, die gelbe Folie ist „3“.
Wenn du nun die beiden Folien übereinander schiebst, siehst du, dass – wenn auch nicht so deutlich wie beim „echten“ Mischen – eine Farbe entsteht, die man durchaus als „Orange“ deuten kann.

Was passiert, wenn ich aus dem Orange (der Acht ) das Rot (die Fünf ) herausziehe?

Und nun, nachdem die Zahlenbeziehungen und der Zusammenhang von Plus und Minus geklärt sind, können auch Minusrechnungen angeschrieben werden.
Dafür greife ich gerne noch einmal auf das Bild des Herausziehens einer Farbe aus der Mischung zurück, weil ich so auch noch eine optische Verbindung zum Rechenzeichen Minus herstelle.

Zu dieser Einführung des Minus findest du in meinem Arbeitsheft für die erste Klasse einige Arbeitsblätter (siehe die Seite Bücher auf diesem Blog).
Das Besondere an diesem Zugang ist, dass dadurch ein Zusammenhang hergestellt wird, der interessantes und abwechslungsreiches Arbeiten möglich macht. und wo auch wieder ohne Denken nichts geht.
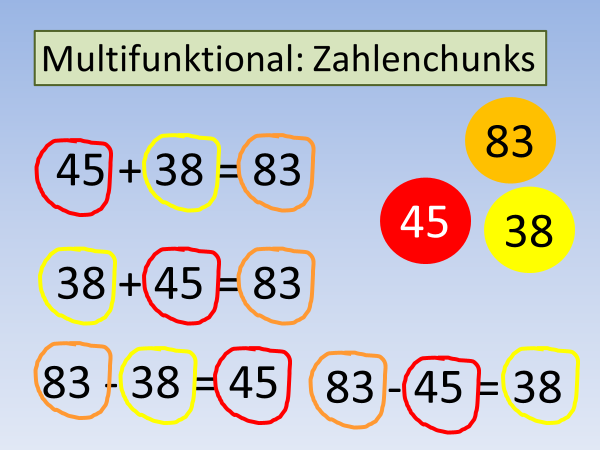
So können zum Beispiel die alten Ästeaufgaben hergenommen werden: Zu jedem Zahlentripel – oder auch Zahlenchunk – gibt es zwei Plus- und zwei Minusaufgaben:

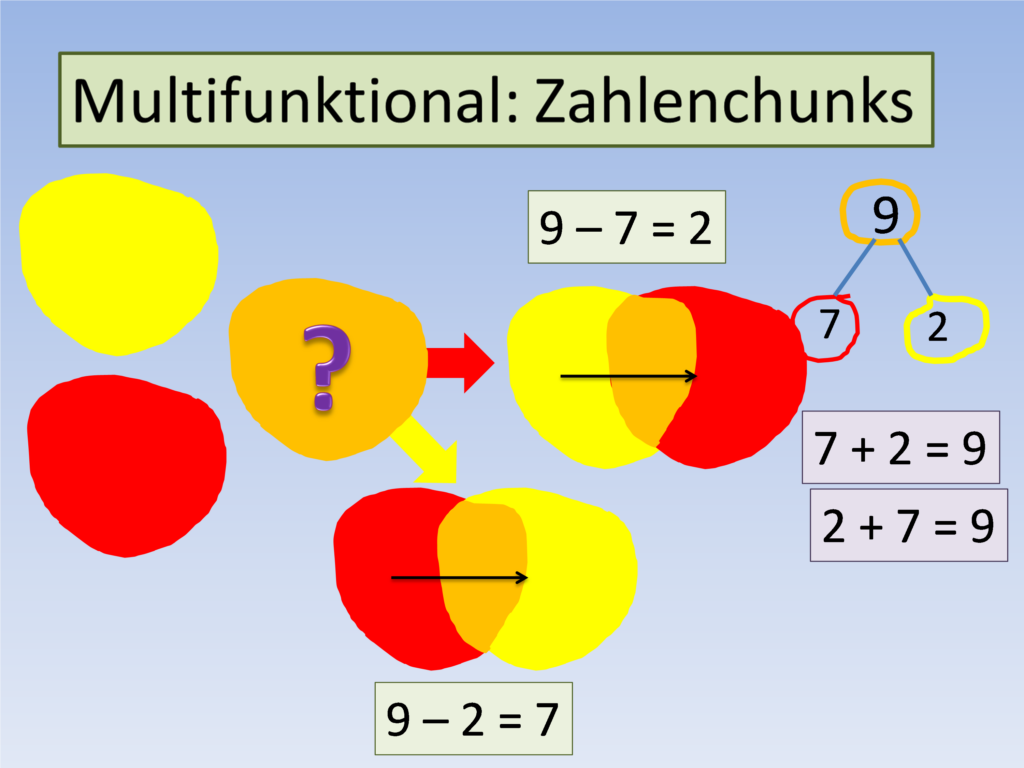
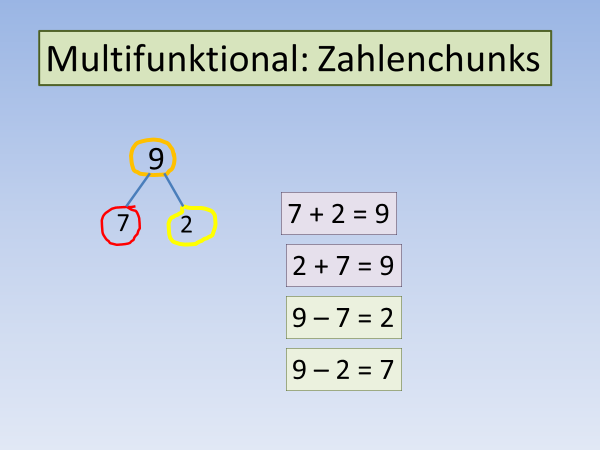
Diese Verbindung zwischen Plus- und Minusaufgaben auf dem Weg über die Zahlenchunks und die Farbenmischung macht auch deutlich, wie das mit den Tausch- und Umkehraufgaben funktioniert:
Ob beim Addieren zuerst Rot oder zuerst Gelb kommt, ist vollkommen gleichgültig, das ist das Prinzip der Tauschaufgaben.
Und wenn ich die gemischten Farben (Rot + Gelb = Orange) wieder ent-mische, habe ich die Umkehraufgabe. Das ist doch viel besser als die Kinder nur mechanisch Umkehraufgaben rechnen zu lassen, ohne das gedankliche Durchdringen der Zusammenhänge.

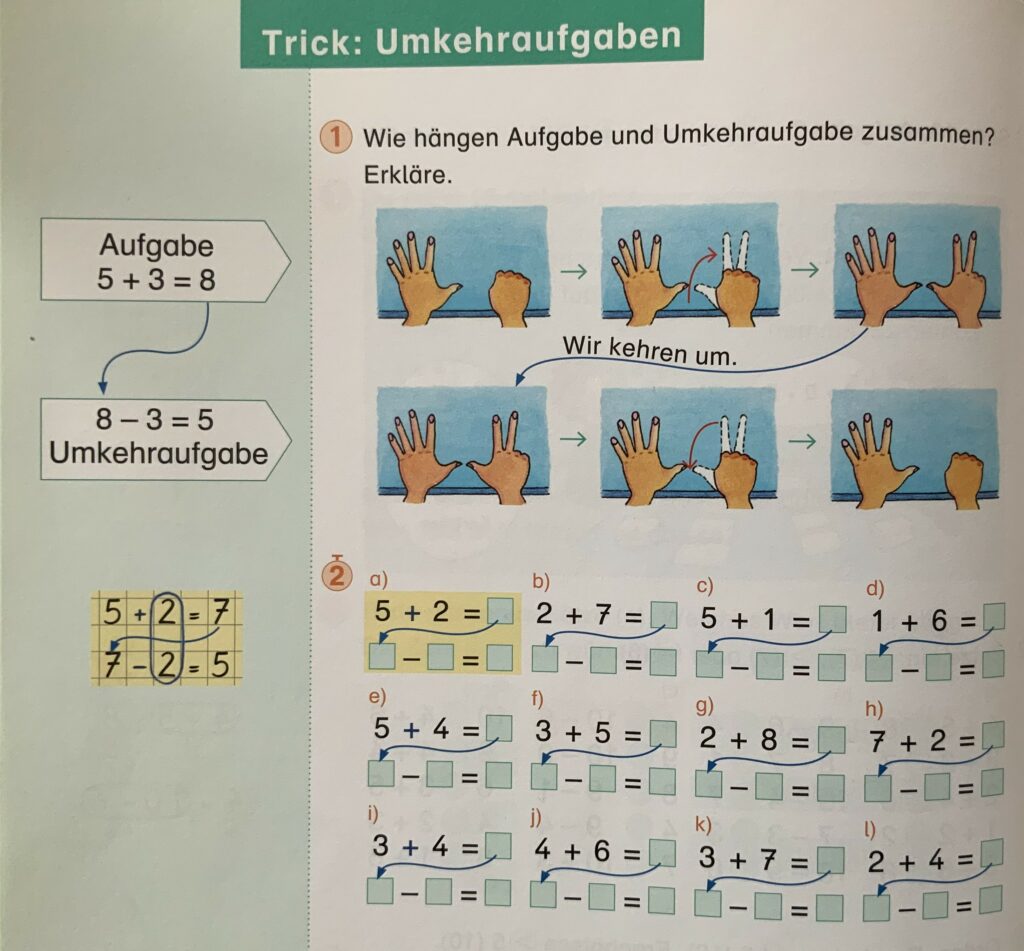
Hier wird das mechanische Nicht-Denken geradezu herausgefordert!

Die Sache mit den Zahlenchunks und den Farben eignet sich übrigens auch für höhere Klassen. Ich habe das zum Beispiel erfolgreich in einer dritten Klasse eingeführt. Da haben manche Kinder zum ersten Mal eine Ahnung bekommen, was das mit den Tausch- und Umkehraufgaben überhaupt soll!

Wie es mit dem Minusrechnen weitergeht, kannst du im nächsten Beitrag nachlesen:
„Erste Schritte beim Rechnen mit Minus“ und dann komme ich sehr schnell zum Subtrahieren mit Zehnerunterschreitung im Beitrag „Minus mit Schnappi“.