Wenn du mit deiner Klasse einen Ziffernschreibkurs machst und den Kindern dafür reichlich Zeit gibst, dann sollten alle jetzt die Zahlen bis fünf schreiben können, je nach Bundesland und Schuljahresbeginn vielleicht auch mehr.
Jetzt ist es Zeit für einen wichtigen Schritt zum weiteren Verständnis der Zahlenwelt.
Rekapitulieren wir:
Die Kinder haben die Reihenfolge der Zahlen durch häufiges Handeln gefestigt.
Sie können die Zahlen bis 5,6, oder 7 schreiben.
Sie können in diesem Umfang auch Mengen bestimmen und im Idealfall sogar noch für eine konkrete Menge den passenden Platz auf der Zahlenreihe finden.
Wenn es nun an das Zerlegen von Zahlen geht, so geschieht – wenn wir das didaktisch richtig anfangen – in den Köpfen der Kinder viel mehr als nur das automatische Einprägen von Zahlenkombinationen.

Diese Zahl sollte im Kopf des Kindes nicht beziehungslos im luftleeren Raum hängen, sondern es sollten sich an sie konkrete Vorstellungsbilder knüpfen.
Beispiel: Zerlegen der Zahl sieben
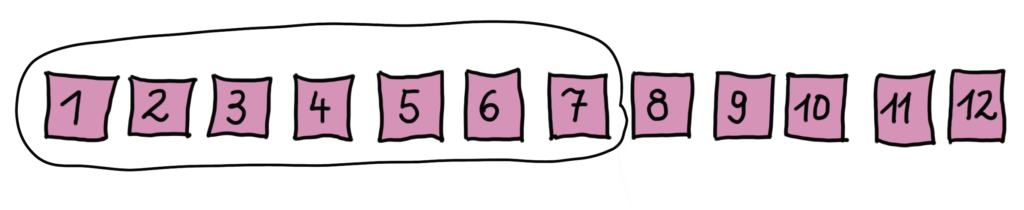
Die Sieben hat ihren festen Platz in der Zahlenreihe.
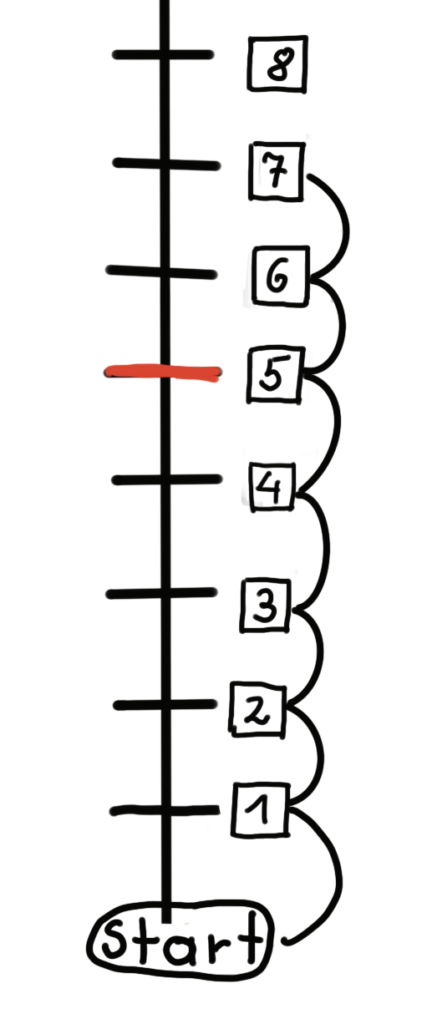
Um bis zur Sieben zu gelangen, musst du vom Start weg genau 7 Schritte gehen.
Plättchen würfeln – ein weiterer Blick in die Systematik der
Zahlenwelt
Das sind genau 7 Rechenplättchen.

Diese 7 Rechenplättchen werden nun in den zusammengelegten hohlen Händen – oder in einem Würfelbecher – fest durcheinandergeschüttelt und auf den Tisch geworfen.
Jetzt kommt das eigentliche Zerlegen


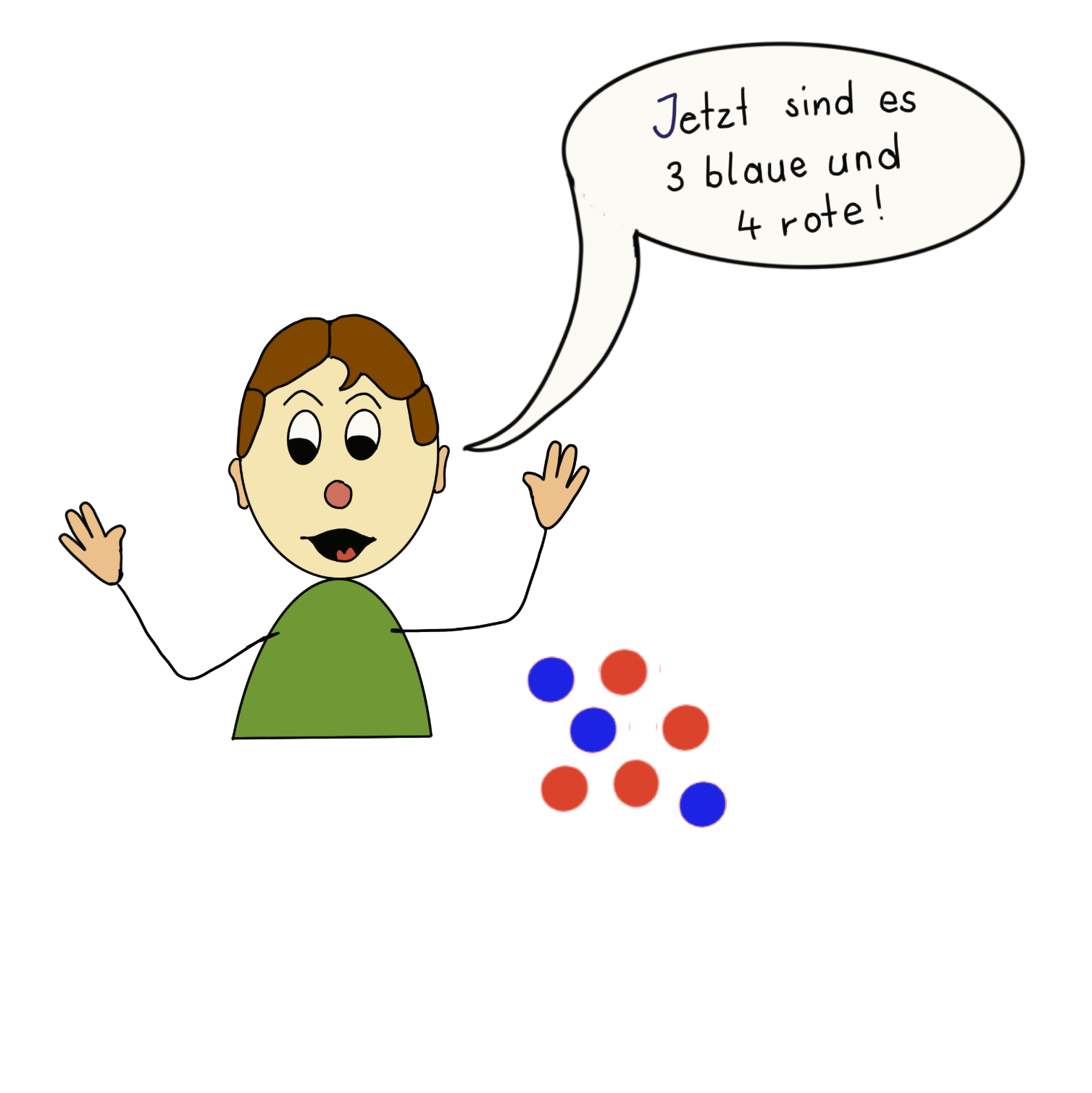
7 Plättchen abzählen ……schütteln ……….. werfen: 3 blaue und 4 rote!
Das Ergebnis wird notiert
Vermeide die hoch abstrakte Notation als Plusaufgabe. Das geht viel einfacher, mit einer „naiven“ Notation, die sehr nahe an der ausgeführten Handlung liegt und im Gehirn nochmal den ganzen Ablauf triggert.
Was genau ist bei diesem handelnden Zerlegen passiert?
Aus einem ungeordneten „Haufen“ von 7 Plättchen ist eine Zweier-Gruppierung aus roten und blauen Plättchen geworden, die nun erst einmal ordentlich gelegt wird.

So……………………………………oder so
Dann wird das Bild in eine Notation mit Zahlen übersetzt.
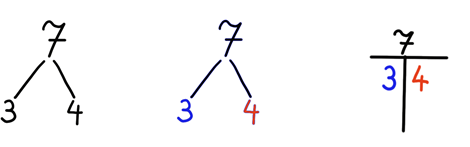
Hier ist deutlich zu sehen: aus dem großen Haufen mit 7 Plättchen werden zwei kleinere Häufchen mit 3 bzw. 4 Plättchen: Links liegen die blauen und rechts die roten Plättchen, das kann auch mit roter und blauer Farbe beim Notieren nochmal betont werden.
So kann es weitergehen:
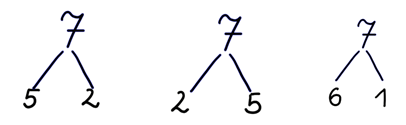
Weitere Zerlegungen werden handelnd erfahren und dann als „Ästediagramm“ notiert.
Ein Überblick über alle möglichen Zerlegungen kann in einer Tabelle notiert werden:
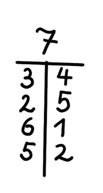
Das alles steckt mathematisch in diesen Zahlenzerlegungen:
Durch häufig wiederholte praktische Zahlenzerlegungen werden mathematische Grundvorstellungen gebahnt. Zunächst einmal wird das Prinzip der Rekursion – eine höchst abstrakte Angelegenheit, die auch nicht allen Lehrern bewusst ist – immer und immer wieder erfahren:

Sieben ist nicht einfach eine einzige Zahl, sondern die Sieben beinhaltet die Menge aller Elemente, die sich auf dem Weg bis hin zur Sieben befinden.
In der Sieben sind Teilmengen enthalten, die zusammen wieder die Menge Sieben ergeben.

Daraus ergibt sich – gleichsam nebenbei – die Erkenntnis, dass mit jedem Schritt weiter die Menge um ein Element größer wird. Acht ist also nicht einfach eine isolierte Acht, sondern es ist ein Element mehr als Sieben.
Je größer eine Zahl ist, desto weiter weg vom Start ist sie auf dem Zahlenstrahl angesiedelt.
Die Ästediagramme zeigen immer eine Dreiergruppe von Zahlen – ein Zahlentripel. Diese Dreiergruppen gehören zusammen und bilden den Ausgangspunkt für spätere Untersuchungen von Zahlenbeziehungen.
Eine weitere Vertiefung – die Darstellung eines Sachverhaltes auf verschiedene Arten
Wenn Kinder unabhängig von der konkreten Darstellung begreifen, was der abstrakte Gehalt einer mathematischen Konstellation ist, dann nennt Aebli diesen Vorgang des Begreifens „Entschlackung“.
Diesen Vorgang des Begreifens können wir fördern durch verschiedene Darstellungen ein und desselben Sachverhalts. Am Beispiel unserer Zahlzerlegungen könnte das so aussehen:
Die Gesamtmenge 7 kann ich zerlegen in zwei Teilmengen: 3 und 4.
Das kann ich nun auf vier verschiedene Arten darstellen:
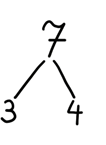
als Ästediagramm…
als kleine Tabelle…
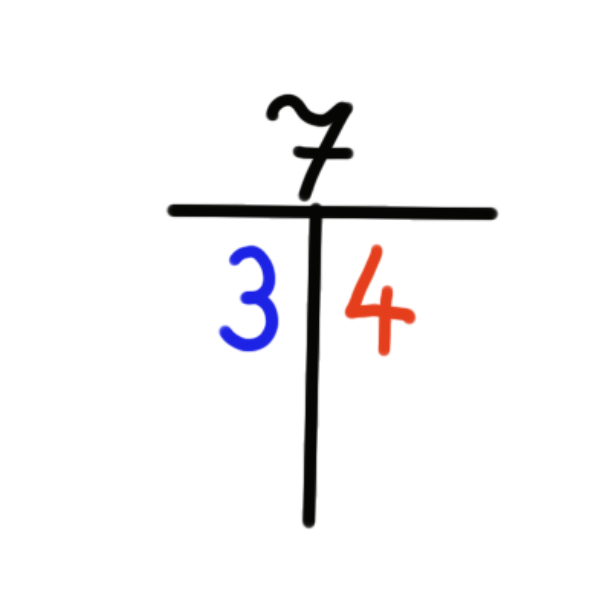

als Punktebild…
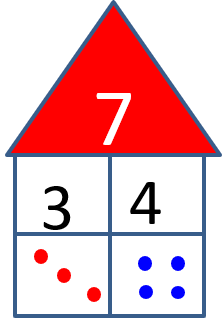
…oder als Zahlen- oder Dominohaus.
Das sieht auf einer Heftseite dann in der Zusammenschau so aus:
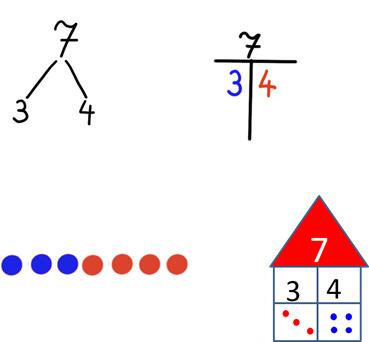
Kinder, die eine Zahlenrelation auf diese vier Arten darstellen können, erbringen eine hohe Abstraktionsleistung. Das ist nicht trivial.
Damit derartige Notationen gut aufgeschrieben werden können, sollten die Kinder nicht durch eine karierte Lineatur eingeengt werden. Ich habe die besten Erfahrungen mit unlinierten A4-Heften gemacht. Das ermöglicht jedem einzelnen Schüler ein Herantasten an seine individuelle Darstellungsweise und führt langfristig zu weit ordentlicherer Heftführung als wenn zu früh bereits eine Einengung durch kariertes Papier auferlegt wird.
Einige Arbeitsblätter zum Thema Zahlzerlegungen kannst du hier herunterladen:
Zahlzerlegung 1
Zahlzerlegung 2
Zahlzerlegung 3
Zahlzerlegung 4