Kinder, die in die Schule kommen, erwarten sich Großes. Sie freuen sich darauf zu lernen und ein richtiges Schulkind zu werden. Die Wirklichkeit aber ist für nicht wenige ABC-Schützen ziemlich ernüchternd. Der Sohn einer befreundeten Kollegin zum Beispiel war vom Anfangsunterricht bitter enttäuscht, weil ihm jede intellektuelle Herausforderung fehlte und er überhaupt nicht das Gefühl hatte, irgend etwas dazuzulernen.
Er meinte, das sei in der Schule wie im Kindergarten. Er müsse immer nur malen und dabei wolle er doch richtig lernen! Dabei wäre es so einfach, ALLE Kinder von Anfang an auf die spannende Entdeckungsreise ins Land des mathematischen Denkens mitzunehmen.
Allerdings geht das nicht so:
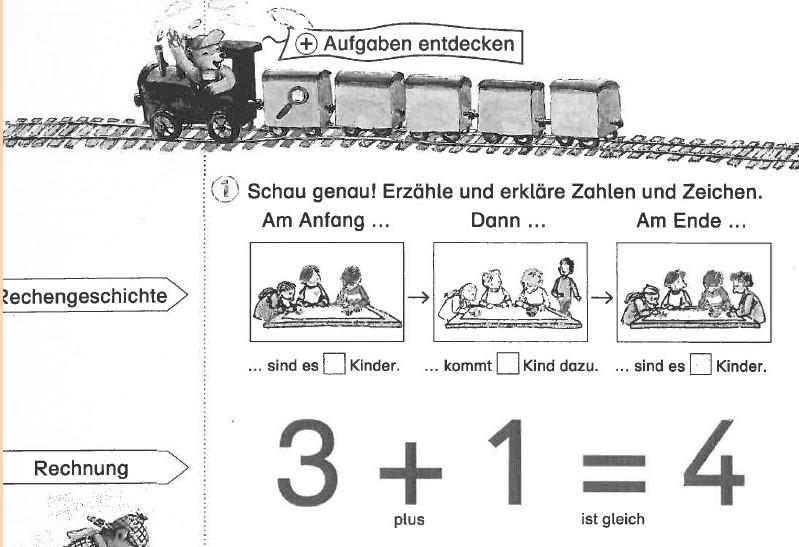
Diese Aufgabenseite aus einem Rechenbuch macht bei ein bisschen kritischem Hinsehen sehr deutlich, wie öde es ist, sich mit ihrem Inhalt beschäftigen zu müssen.
Die Rechnung 3 + 1 ist denkbar trivial, durch schlichtes Weiterzählen um eins zu lösen und überhaupt nichts, was mathematisches Verständnis fördert und schon gleich gar keine Motivation zum Nachdenken.
Die Zielsetzung „Aufgaben entdecken“ ist eine euphemistische Übertreibung. Der Text, der eine Anleitung zum „Entdecken“ der Aufgabe 3+1 sein soll, ist von Erstklässlern kurz nach Schuljahresbeginn noch gar nicht zu lesen und die drei Bilder sind alles andere als deutlich.
Und was gibt es denn da überhaupt zu entdecken?
Dann bleibt auch noch die Tatsache, dass bei aller inhaltlichen und zahlenmäßigen Plattheit dieser Aufgabe die abstrakte Rechensprache einer Gleichung beileibe nicht auf Anhieb jedem Schulanfänger sofort einsichtig ist.
So haben wir die absurde Situation, dass die Inhalte des Rechenunterrichts für viele Kinder langweilig sind – also unter-fordernd – und der sofortige Einsatz der abstrakten mathematischen Zeichensprache nicht wirklich verstanden wird, also über-fordernd ist. Widersprüchliche Botschaften sind in der Pädagogik unbedingt zu vermeiden, das wissen wir doch alle „eigentlich“.
Wenn es dann so weitergeht wie mit dem folgenden Blatt – immer noch im Zahlenraum bis 5 – wird die Verwirrung mit den abstrakten Zeichen nicht kleiner und die Langeweile mit den immer gleichen Zahlen nicht geringer:
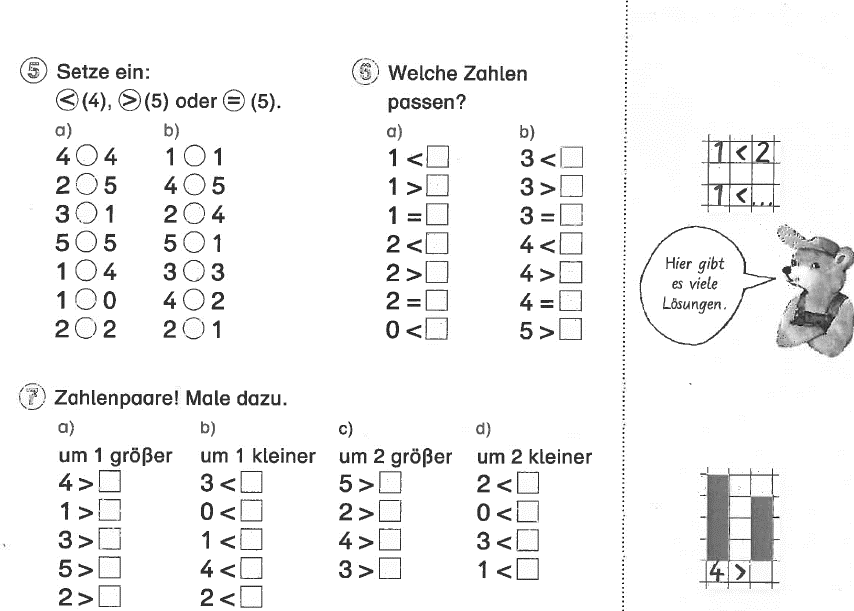
Da hilft auch der Bär nicht weiter, der – wohl als Motivierungsversuch – behauptet, hier gäbe es viele Lösungen.
Deine Chance: Du kannst dich jetzt gedanklich damit befassen, wie du mit deiner ersten Klasse in das neue Schuljahr starten möchtest! Pack den Mathe-Stier bei den Hörnern, lass das Rechenbuch Rechenbuch sein und geh mit deinen Schülern den Weg des Denkvergnügens!
Statt Mathebuch:
Öffne von Anfang an den Zahlenraum bis 20!
Zähle und spiele zuerst einmal in diesem Zahlenraum mit den Kindern.

Die Zahlenreihe wird dadurch lebendig für die Kinder und somit auch
be-greifbar.
Das ist viel mehr als das bloße Aufsagen einer Reihe von Zahlwörtern. Zahlreiche Anregungen dafür findest du auf diesem Blog hier!
Naive Notationen – der Königsweg für die denkende Auseinandersetzung mit Aufgaben im Zahlenraum bis 20
Neben den Spielen mit der Zahlenreihe musst du natürlich daran arbeiten, dass die Kinder die Ziffern 1 bis 9 schreiben lernen. Wenn ihr bei der 5 angelangt seid, können schon die ersten Zahlzerlegungen notiert werden und zwar ganz naiv, sozusagen als vereinfachtes Abbild dessen, was passiert:


Hier hält Sabine 7 rot-blaue Wendeplättchen in den Händen, schüttelt und lässt sie auf den Tisch fallen. Es zeigt sich die Zerlegung in 2 blaue und 5 rote Plättchen.
Dieses Ergebnis wird nun nicht als Gleichung notiert, sondern „naiv“ als Ästeaufgabe:
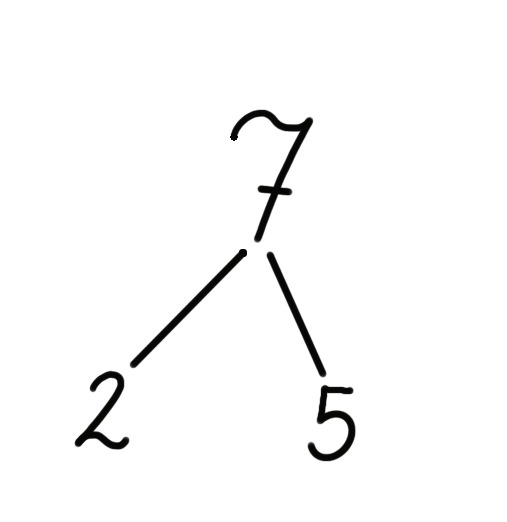
In dieser Notation ist die Handlung noch zu erkennen: Aus einer einzigen Menge von 7 Plättchen werden zwei Teilmengen: 2 und 5
Diese Notation versteht jedes Kind auf Anhieb. Später kann die Äste-Notation noch ergänuzt werden durch eine Tabelle, ein Zahlenhaus und ein Punktebild.

Hier sehen wir Notationen aus einem Schülerheft mit der Zerlegung 5 blaue und 2 rote Plättchen.
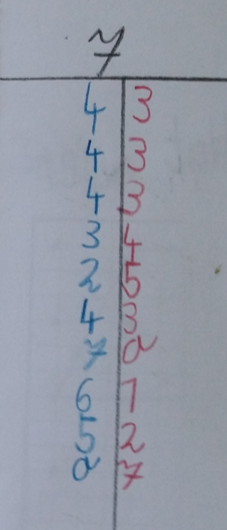
In dieser Tabelle sind viele Würfe mit 7 Plättchen notiert: Links die blauen, rechts die roten Plättchen.
Die ersten 3 Würfe fielen gleich aus.
Ein weiterer Zugang zu Zahlen: Punktebilder legen und malen
Die Anregung hierzu stammt von Wittmann/Müller:
Begleitend zum Ziffernschreibkurs kannst du an Mengendarstellungen arbeiten, wie zum Beispiel an Punktebildern.
Diese Punktebilder werden zuerst mit den Wendeplättchen gelegt und dann mit der Schablone ins Heft gezeichnet. Je mehr Plättchen verwendet werden, desto mehr Variationen sind möglich.
Du kannst z.B. eine Zahl vorgeben mit dem Auftrag, so viele verschiedene Punktebilder wie möglich mit dieser Anzahl von Wendeplättchen zu legen.

Hier hat eine meiner Schülerinnen mit verschiedenen Plättchenmengen experimentiert.
Mengendarstellungen von 1 bis 9

Blankobierdeckel werden beschriftet und mit Pfeifenreinigern versehen, auf die man die entsprechende Perlenmenge fädeln kann.
Einfach, schnell hergestellt, billig und sinnvoll!
Konkrete Mengen mit Bildern und Gegenständen

Im Freiarbeitsregal können z.B. folgende „Blankomengen“ liegen:
Eine Moosgummiwiese, ein Vogelnest, ein Spinnennetz, ein Salatkopf.

Zu diesen „Blankomengen“ gibt es passende Figuren oder Bilder.
Eine Zahlenkarte wird gezogen.

Jetzt können die Blankomengen passend zur Zahlenkarte bestückt werden:

Über den Ziffernschreibkurs werde ich demnächst berichten. Für die Planung eines erfolgreichen Einstiegs in das Rechenjahr mit deiner Klasse bekommst du auch noch Impulse in folgenden Beiträgen:
Der Einstieg in die Mathelaufbahn und Zahlen – Freunde, Feinde oder Aliens.