Die Steinzeit ist uns näher als du glaubst
Unser Gehirn ist ein faszinierendes Gebilde. Anders als bei technischen Geräten, die sich abnutzen und irgendwann verbraucht sind, läuft unser Hirn bei häufigem und intensivem Gebrauch erst zur Hochform auf: Es wird durch Benutzen schneller und leistungsfähiger.
Die Kehrseite davon ist: Wenn wir es nicht benutzen, baut es ab, es schrumpft gewissermaßen.
Deshalb der Gehirn-Slogan: Use it or lose it!
Nun haben wir im Gehirn zwar gewisse Spezialgebiete, die bei den unterschiedlichen Tätigkeiten besonders aktiv werden. Doch diese Spezialisierungen sind nicht augerichtet auf das Leben, wie wir es führen. Sie stammen aus einer weit zurückliegenden Zeit der Menschheitsgeschichte, „from the caves“, wie Daniel Whiteside in seinen Seminaren immer sagte.
Die grundsätzliche genetische Umprogrammierung des Gehirns und die bereits im Erbgut angelegte Anpassung an veränderte Lebensbedingungen dauert sehr lange, ca. 100 000 Jahre.

Sprache dient den Menschen schon sehr lange zur Verständigung, da konnte unser Gehirn sich darauf einstellen und sich genetisch anpassen.
So haben wir zwar zwei Gehirnbereiche, die auf Sprache spezialisiert sind – Wernickezentrum für Sprachverständnis und Brocazentrum für Sprechmotorik — aber wir haben kein Lesegehirn, kein Schreibgehirn und auch kein Rechengehirn!
Die Kulturtechniken Lesen, Schreiben und Rechnen sind – gemessen an der Entwicklungsgeschichte der Menschheit – noch sehr jung, lächerlich wenige tausend Jahre.
Und trotzdem: Wir sind in der Lage, diese Techniken zu erlernen. Unser Gehirn ist nämlich sehr findig bei der Einstellung auf veränderte Bedingungen und bei der Anpassung an das aktuell Notwendige. Neuroplastizität heißt das Stichwort (Lesetipp: Bücher von Norman Doidge).
Es nimmt einfach das, was schon da ist, und macht das Beste daraus.
Unser Gehirn – das Schweizer Taschenmesser
Was macht ein guter Mechaniker, wenn er vor einem Problem steht und nicht ein genau passendes Ersatzteil oder Spezialwerkzeug hat? Er sucht sich etwas, das – wenn auch zweckentfremdet – als Werkzeug oder Ersatzteil dienen könnte.
So wird zum Beispiel in unserer Familie folgende Anekdote aus lange zurückliegenden Zeiten erzählt, als Autos noch mechanisch repariert werden konnten:
Meine Schwiegereltern und eine Freundin waren mit dem Auto – noch zu DDR-Zeiten – unterwegs von Bayern nach West-Berlin. Mit an Bord war Kalle, ein sehr begabter Automechaniker. Auf der Autobahn Ost riss der Keilriemen und das warf gewaltige Probleme auf: Es war nicht erlaubt, die Transitstraßen zu verlassen, Pannenhilfe gab es nicht und Handys natürlich auch noch nicht. Kalle, der Mechniker, ließ sich von einer der mitfahrenden Damen einen Nylonstrumpf geben und baute diesen anstelle des gerissenen Keilriemens ein. Die Behelfslösung funktionierte, man schaffte es bis Westberlin und in eine richtige Werkstatt.
Genau so, wie der findige Mechaniker Kalle den Damenstrumpf zu einem Keilriemen umfunktionierte, benutzt auch unser Gehirn bereits vorhandene Funktionen, die sich gut zum Rechnen – oder Schreiben und Lesen – eignen.
Nun ist das allerdings so, dass nicht von jedem Gehirn die optimal passenden Funktionen benutzt werden, sondern es wird manchmal ein sehr mühsamer und unpraktischer Umweg gemacht.
Wenn wir das aber verstehen und wenn wir wissen, welche Wege die günstigsten sind, dann können wir nicht nur Kindern, die sich schwer tun, sondern überhaupt allen Kindern, die wir im Rechnen unterrichten, den Zugang zu dieser anspruchsvollen und abstrakten Disziplin wesentlich erleichtern.
Wo die Zahlen wohnen
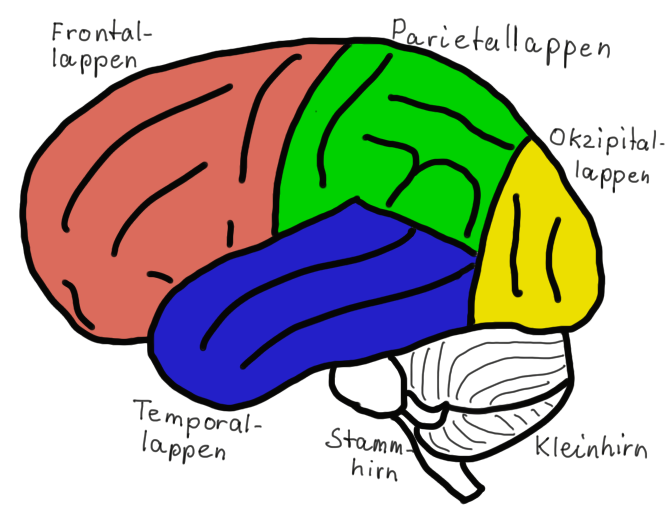
In der Großhirnrinde sind die verschiedenen Bereiche verschiedenen Funktionen zugeordnet:
Frontallappen u.a. Pläne, Organisationen, Verantwortung, Bewegungssteuerung, Sprachmotorik
Temporallappen u.a. Riechen, Hören, Sprechen, Verstehen, Gedächtnis,
Parietallappen u.a. Sensorik, Motorik, Propriozeption, Raumorientierung, Bewegungsabläufe, Analyse von Bewegungsabläufen, Wahrnehmungsintegration von Sehen, Hören, Gleichgewicht, mentaler Zahlenstrahl,
Okzipitallappen Sehzentrum
Besondere Bedeutung für die Rechenfähigkeit besitzt ein bestimmter Bereich des Parietallappens: Der intraparietale sulcus, kurz: IPS.
Sulcus ist ein Graben in den Windungen unseres Gehirns.
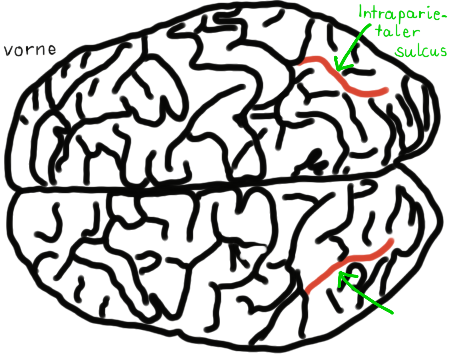
Karin Kucian hat an der Universität Zürich vor mehr als 15 Jahren begonnen, dem Gehirn von Kindern mit funktioneller Magnetresonanztomografie (fMRT) beim Rechnen zuzuschauen und dabei festgestellt, dass bei guten Rechnern dann, wenn sie Aufgaben lösten, besonders große Aktivität im IPS festzustellen war, während bei schwachen Rechnern die Aktivitäten verteilt auf verschiedene Gehirnbereiche, aber kaum im IPS zu beobachten waren.
Unser schlaues Gehirn nimmt einfach, was da ist und macht das Beste daraus
Unser Steinzeitkollege musste noch nicht rechnen, aber es war für ihn überlebenswichtig, sich räumlich zu orientieren. Wo gibt es Mammuts? Wo finden wir Pilze, Kräuter und Beeren? Wie komme ich zu meiner Höhle zurück? Welche Wege muss ich gehen?
Die unendliche Zahlenreihe hat Ähnlichkeit mit einer Straße: Sie ist ein räumliches Gebilde, in dem manches näher da und anderes weiter entfernt ist. Wer sich auf dieser Zahlenstraße gut orientieren kann, ist in der Lage, sehr schnell zu entscheiden, welche von zwei Zahlen die größere ist, ob er vorwärts oder rückwärts gehen und denken muss. Er hat ein Referenzsystem, auf das er Bezug nehmen kann. Es ist sehr schlau von unserem Gehirn, die räumlichen Fähigkeiten, die ja genetisch schon angelegt sind, für diese Orientierung zu nutzen. Gute Rechner machen das auch, und den schwachen Rechnern müssen wir dazu verhelfen.
In der Folge von den Erkenntnissen, die Karin Kucian gewonnen hatte, gab es einige Studien über die Wirkung von gezielter Stimulation des IPS auf die mathematischen Fähigkeiten. So berichtete die Süddeutsche Zeitung am 5.11.2010 über Versuche mit transkranieller Gleichstromstimulation. Die Rechenleistungen der Probanden waren nach der Versuchsreihe deutlich besser und diese Besserung hielt 6 Monate an.
Auch der Spiegel berichtete darüber.
Was nützen uns diese Erkenntnisse in der Praxis?
Natürlich können wir keine teuren und groß angelegten Studien mit unseren Schülern durchführen. Das wäre in meinen Augen auch gar nicht sinnvoll.
Was aber für uns höchst wertvoll ist, das sind die daraus abzuleitenden Erklärungen, warum manche didaktischen Wege im Alltag so gut funktionieren und andere wiederum eher nicht. Wenn wir ein Kind vor uns haben, das sich in der Zahlenwelt nicht orientieren kann, dann sind für dieses Kind und für seine Eltern Studien und wissenschaftliche Erkenntnisse gleichgültig.
Sie wünschen sich nur eines sehnlichst: Dass das mathematische Elend ein Ende hat.
Und das, was über die Auswirkungen der Elektrostimulation auf bestimmte Gehirnbereiche festgestellt wurde, könnte uns doch auf die Idee bringen, diese Gehirnbereiche in unserem Unterricht gezielt zu aktivieren, mit einfachen Tätigkeiten, die dort verortet sind.
Wie wäre es denn, wenn wir alles, was mit Bewegung, mit echten Handlungsabläufen, mit räumlicher Orientierung, mit Propriozeption und Wahrnehmungskoordinierung zu tun hat, gezielt mit mathematischen Aktivitäten verknüpfen würden?
Und wie wäre es, wenn wir die Bedeutung des mentalen Zahlenstrahls für das Rechnen auch in unserem Unterricht zur Kenntnis nehmen würden und diese wichtige Orientierungshilfe ganz gezielt an den Anfang unserer mathematischen Bemühungen stellen würden?
Individuelle Evidenzbasiertheit – eine seriöse Sache!
Nun berichte ich aus meiner Praxis, von meinen individuellen Erfahrungen, die nicht „wissenschaftlich“ sind, dafür aber sind sie echt.
Als ich vor vielen Jahren feststellte, dass es mir in einem herkömmlichen Rechenunterricht nicht gelang, allen Kindern zu helfen, das Rechnen in einem befriedigenden Ausmaß zu lernen, machte ich mich auf die Suche nach Alternativen.
Besonders halfen mir dabei die Bücher von Wittmann und Müller (Handbuch produktiver Rechenübungen 1 und 2), die Schriften von Hans Aebli (Grundlagen des Lehrens u.a.) und die Edukinestetik-Kurse von Paul Dennison.
Ich zog für meine Praxis folgende Schlüsse – sozusagen als Arbeitshypothese
- Rechnen darf niemals so gestaltet werden, dass es praktisch „ohne Denken“ funktioniert
- Rechnen darf nicht nur zweidimensional auf dem Papier ablaufen
- Die Zahlenreihe als Bezugspunkt zur „Größe“ von Zahlen hat eine zentrale Bedeutung
- Bewegung spielt beim Rechnenlernen eine Schlüsselrolle
- Rechnen muss mit positiven Emotionen verbunden werden
Dann krempelte ich meinen Unterricht total um und schaute einfach, was passiert. Das Ergebnis war so überzeugend, dass ich auf dem eingeschlagenen Weg seither geblieben bin. Natürlich ist zu den allerersten Schritten sehr viel dazugekommen, aber die grundlegende Richtung hat sich nicht geändert.
All das, was ich hier an didaktischen Ideen und Vorschlägen präsentiere, habe ich vielfach in der Praxis erprobt, in einigen tausend Rechenstunden und mit mehreren hundert Kindern. Der Maßstab für alles war immer: Hilft es oder hilft es nicht?
Und diese individuell evidenzbasierte Vorgehensweise kann meines Erachtens ohne weiteres Schritt halten mit diversen wissenschaftlichen Studien.
Ich wende diese Vorgehensweise sowohl beim Unterricht mit einer ganzen Lerngruppe an als auch bei der Einzelarbeit:
| Hypothese | Intervention | Evaluation des Ergebnisses | Fortfahren oder Abändern |
| Welches Verfahren ist hier das Richtige? Was könnte bei Schwierigkeiten helfen? | Praktisches Vorgehen, z.B. Arbeit am Stellenwertsystem, beim Aufbau von Zahlenbeziehungen, am Zehnerübergang usw. | Bin ich mit dem Ergebnis zufrieden? Haben meine Schüler Fortschritte gemacht? Sind sie motiviert? | Ich kann auf diesem Weg weitermachen oder Ich muss neu überlegen, was zu tun ist. |
Das A und O: Ein gut ausgestatteter Werkzeugkasten
Je mehr wir uns auf den Weg des handlungsorientierten Rechnens einlassen, desto mehr Möglichkeiten haben wir, die wir geplant, aber auch ad hoc einsetzen können. Einige davon will ich aufzählen:
- Aufbau des mentalen Zahlenstrahls durch Bewegung im dreidimensionalen Raum
- Schaffen von Bildern und Bezugsgrößen zum Verinnerlichen des Stellenwertsystems
- Verständnis von Sachaufgaben durch Situationsmodelle
- Zahlenzerlegungen handelnd durchführen, begreifen und speichern
- Stellenwertübergänge sichtbar, greifbar und nachvollziehbar machen
- Emotionale Beteiligung durch gemeinsames Handeln, Spielen und durch „Storytelling“
- und viele weitere
Über alles, was unser mathematischer Werkzeugkasten aus meiner Sicht braucht, werde ich in diesem Blog schreiben, einiges davon findet ihr bereits jetzt.
