Beim Coachingplan ist das Zeitmanagement eine wichtige Sache. Die zweite wichtige Sache ist natürlich das passgenaue Auswählen der Inhalte.
Wenn ein Drittklässler keine Vorstellung vom Dezimalsystem hat und keine Rechenbausteine in Form von Zerlegungen und Auffüllungen auswendig zur Verfügung hat, dann nützt es sehr wenig, ihn Aufgaben aus dem Arbeitsheft der 3. Klasse lösen zu lassen.
Immer mehr vom Selben ist keine erfolgversprechende Strategie.
Du musst erst einmal schauen, wo genau dein Schüler vom mathematisch rechten Weg abgekommen ist. Ich nenne dir jetzt einige fundamentale Bausteine, die vorhanden sein müssen, damit überhaupt „echt“ gerechnet werden kann.
Dass alles nur dann einen Sinn hat, wenn ein Kind selber will, ist die conditio sine qua non, das muss klar sein, sonst sind Zeit, Geld und Mühe verschwendet.

Mathematik ist ein Fach, dessen Inhalte hierarchisch aufgebaut sind. Das ist anders als bei einer Fremdsprache. Selbst wenn du eine Reihe von Wörtern nicht kannst oder bestimmte grammatikalische Konstruktionen nicht aktiv anwenden kannst, so heißt das nicht, dass du überhaupt nichts verstehen kannst.
Ganz anders in Mathematik! Da ist es so, dass du, wenn dir die grundlegenden Bausteine fehlen, nur orientierungslos herumirren und raten kannst. Und genau das ist der Zustand, in dem viele Schüler den Rechenunterricht mehr er-leiden als erleben.
Die Bausteine
- Orientierung im Zahlenraum
Zu dieser Thematik kannst du dich genauer informieren in verschiedenen Beiträgen auf diesem Blog:
Über verschiedene Zahlaspekte, über die Geschichte der Zahlen, über Handlungsmöglichkeiten mit der Zahlenreihe und über den mentalen Zahlenstrahl.
Wer sich im Zahlenraum bis 20, 100 oder 1000 orientieren kann, ist in der Lage,
– auf Anhieb zu sagen, welche von zwei Zahlen größer ist,
– drei oder mehr Zahlen der Größe nach zu ordnen,
– auf dem Zahlenstrahl Zahlen zu finden, die genannt werden (Wo ist die 732?) – auch wenn der Zahlenstrahl nur intervallisch beschriftet ist,
– Strukturen zu nutzen beim intervallischen Zählen, z.B. ab 46 in Zehnerschritten oder ab 135 in Hunderterschritten - Zahlenzerlegungen bis 10
Alle Zahlenzerlegungen müssen auf Anhieb verfügbar sein:
Zerlege die 7 in zwei beliebige Häufchen!
Wenn ich die 9 in zwei Häufchen zerlege und das eine Häufchen ist 5, wie groß ist das andere? - Auffüllen zu Stellenwertgrenzen
Von einer beliebigen Zahl wird bis zum nächsten Zehner, Hunderter oder Tausender aufgefüllt.
Über die Bedeutung der Stellenwerte gibt es bereits einen Beitrag. - Stellenwertüberschreitungen
Plus- oder Minusrechnungen mit Zehnerüberschreitung im Zahlenraum bis 20 können mit Zerlegung und Auffüllung (oder bei minus mit Zerlegung des Subtrahenden und im zweiten Schritt mit Öffnung des Zehnerbündels) durchgeführt und erklärt werden – (Wie hast du’s genau gemacht?).
Rechnungen im Hunderter- oder Tausenderraum können halbschriftlich in zwei oder drei Teilschritten gelöst und erklärt werden. - Dezimalsystem
Der Unterschied zwischen Zehnern, Hundertern und Tausendern ist verstanden und kann erklärt werden: Warum ist bei 279 die Zwei am meisten wert? - Zahlentripel als Superbausteine
Bei Zahlenzerlegungen entsteht ein Dreiergefüge aus Zahlen, die zueinander in Beziehung stehen.
Diese Zahlentripel sind als Superbausteine wichtig, denn in ihnen stecken jeweils zwei Plus- und zwei Minusaufgaben.
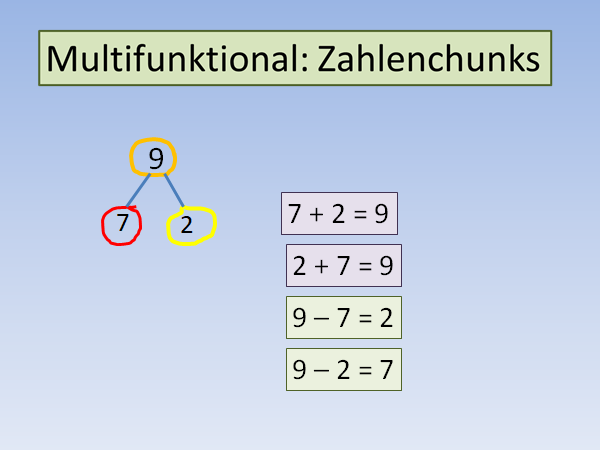
- Grundvorstellungen Plus und Minus
Was gescheht genau bei Plus und was bei Minus?
Kannst du zu einer Plus- bzw. Minusaufgabe eine kleine Rechengeschichte erfinden?
Diese Bausteine müssen unbedingt erworben werden, bevor es ans Malnehmen und Teilen und an die schriftlichen Rechenverfahren geht.
Aufbau einer Coaching-Etappe
Du hast als zeitliche Planungsgrundlage das Uhrenbuch, in das jede Trainingsviertelstunde eingetragen wird.
Du musst bei der Planung bis zu dem Niveau zurückgehen, an dem dein Schüler noch Boden unter den Füßen hat. Von dort aus kannst du dann das Training aufbauen. In meinen Coachings hat es sich bewährt, Teilziele festzusetzen und dann mit zwei, maximal drei verschiedenen Schwierigkeitsstufen zu starten.
Beispiel: Die Zahlenzerlegungen der Zahlen bis Zehn sollen erarbeitet und gefestigt werden.
Woche 1
Du kannst das darunterliegende Thema „Orientierung im Zahlenraum“ dazunehmen und die Trainigsviertelstunde mit einem Spiel im Zahlenraum beginnen, z.B.
Die schlimme Sieben,
Afrikanisches Memory,
Räuber und Goldschatz,
Kuhschwanz,
Streichholzpoker.
Danach zerlegt dein Schüler Zahlen handelnd, z.B. durch Werfen mit den Wendeplättchen, und notiert die Ergebnisse.
Woche 2
Beginne wieder mit einem Spiel.
Die Zahlen werden handelnd zerlegt und die Ergebnisse auf verschiedene Arten notiert:
Als Ästeaufgabe, als Tabelle, als Zahlenhaus und als Punktebild.
Woche 3
Dein Schüler arbeitet abwechselnd mit zwei Aufgabenstellungen:
Eine Zahl wird handelnd zerlegt und das Ergebnis notiert, einmal als Ästeaufgabe, einmal als Mini-Tabelle, einmal als Zahlenhaus.
Eine unvollkommene Zerlegung wird ergänzt, entweder auswendig oder durch das kluge Legen von Plättchen, z.B.:
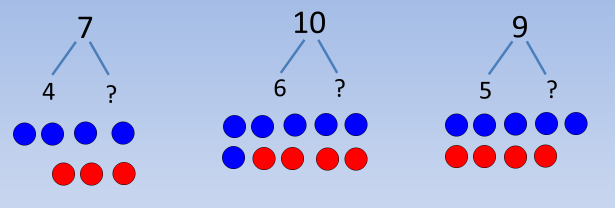
Die bekannte Zahl wird zuerst blau gelegt, danach wird rot ergänzt auf die „Kopfzahl“
Diese beiden Aufgabenstellungen wechseln sich ab.
Zum Schluss ein Spiel mit Zahlenzerlegungen:
Es werden 5 oder 10 Chips in die Mitte gelegt.
Du nennst eine unvollständige Zerlegung, z.B: 8 – 5 – ?
Dein Schüler nennt die fehlende Zahl richtig und bekommt einen Chip.
Gespielt wird, bis alle Chips gewonnen wurden.
Variante:
Die Fehlversuche werden eigens gezählt. Das Ziel ist es, diese auf Null zu reduzieren.
Weitere Spielmöglichkeit – Zerlegungsmemory:
Du hast zwei Sorten von Karten (selbst gemacht). Auf einer Sorte stehen unvollständige Zerlegungen, auf der anderen Sorte nur Zahlen zwischen 1 und 9. Es sollen passende Paare gefunden werden.
Die eine Sorte ist auf der Rückseite mit einem Punkt markiert, die andere blanko.
Woche 4
Dein Schüler bekommt unvollständige Zerlegungen in Form von Tabellen und soll sie ergänzen.
Wie viele Aufgaben schafft er in 5 Minuten?
Es werden zu Ästeaufgaben die zwei passenden Plus- und Minusaufgaben gesucht.
Ein neues Ziel wird gesetzt
Wenn die Zahlenzerlegungen sitzen, kann mit neuen Zielen gearbeitet werden. Passende Anschlussinhalte wären hier:
Auffüllen zu Zehner- oder Hundertergrenzen, Platzhalteraufgaben mit Besinnung auf die Zahlenzerlegung, die hier zum Einsatz kommt, z.B. 5 + ___ = 8. Die Zerlegung, die du hier brauchst, heißt 8 – 5 – 3.
Diese Reflexion ist sinnvoll, weil den Kindern dadurch bewusst gemacht wird, dass sie bereits erworbene Bausteine verwenden können und nicht jedes Mal alles aufs Neue rechnen müssen.
