Ich bin Schnappi, das kleine Krokodil,
komm aus Ägypten, das liegt direkt am Nil.
Zuerst lag ich in einem Ei,
dann schni-schna-schnappte ich mich frei.
Schni-schna-schnappi, schnappi schnappi schnapp
Schni-schna-schnappi, schnappi schnappi schnapp
Jetzt wird’s richtig spannend!
Wenn du eine verständnisbasierte Vorarbeit geleistet hast, dann wissen deine Schüler, was bei Minus passiert und sie werden auch nicht, wie der arme Kerl auf dem Bild, ihr Heil darin suchen, bei einer Minusrechnung einfach nur – und dazu noch falsch!! – rückwärts zu zählen.
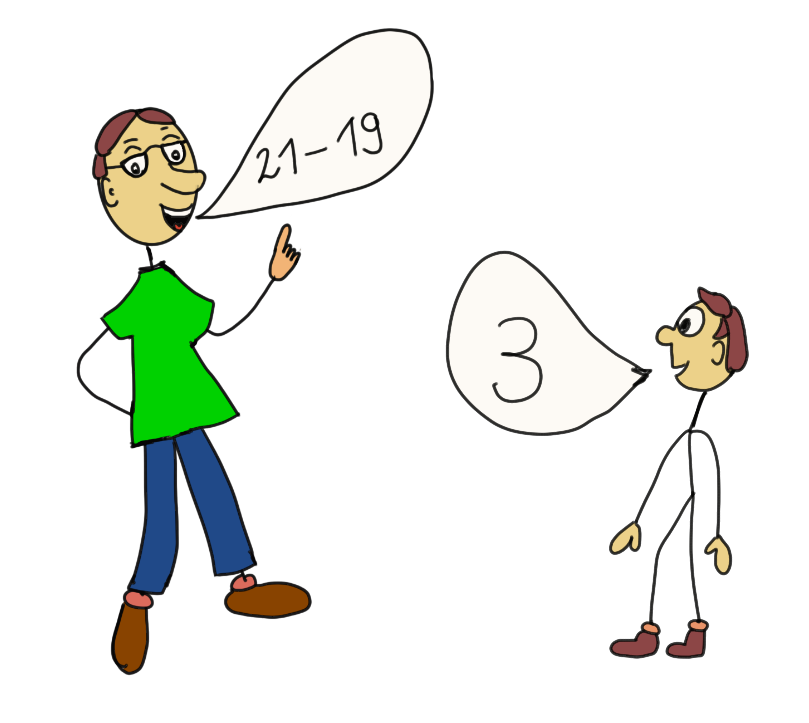
Der Arme! Er denkt sich: 21-20-19! Da braucht er 3 Finger und hält das für das Ergebnis.
Er kann’s nicht besser!
Es macht ja viel mehr Rechenspaß, wenn die Kinder wissen, was sie tun, wenn sie handeln können und dann voller Stolz feststellen, dass sie alles verstanden haben.
Also legen wir los mit einer Beispielrechnung:
14 – 6 =
Kinder, die nur auf ein Ergebnis fixiert sind, ohne das Ganze zu verstehen – und sich bis hierher damit durchmogeln konnten -, werden nun wahrscheinlich, wie der Bub auf unserem Bild – ob mit Hilfe der Finger oder mit einer anderen Zählstrategie – das Ergebnis mechanisch durch Rückwärtszählen ermitteln.
Dabei geschehen oft Fehler durch Verzählen um 1:
14 – 13 – 12 – 11 – 10 – 9: Hier sind 6 Zahlen „zurückgespult“ worden, allerdings, da eben ohne Verständnis, fälschlicherweise unter Einbeziehung der 14, sodass statt des richtigen Ergebnisses „8“ die ver-„rechnete“ Version „9“ herauskommt.
Viele Lehrkräfte fallen auf diese Ersatzstrategie insofern herein, als sie das um Eins verschobene Ergebnis wirklich als geringfügigen „Rechen“-Fehler und nicht als ganz gravierendes Verständnisproblem interpretieren.
In dieser Aufgabe stecken einige Verständnishürden, die bei einem verständnisbasierten Rechenunterricht sofort erkannt werden, die aber bei einem bloß ergebnisfixierten Unterricht für viele Kinder unüberwindbar sind:
- Der Zehner stellt eine Grenze dar, an der wir kurz innehalten müssen.
- Wir können nur 4 ohne Probleme von der 14 abziehen.
- Deshalb müssen wir die 6 zerlegen in 4 + 2
- Damit wir die 2 abziehen können, müssen wir die Zehnergrenze öffnen, das bedeutet, wir müssen die 10 ent-bündeln. Dieses Ent-Bündeln ist wesentlich schwieriger als das Bündeln. Darum ist die Handlungsmöglichkeit so wichtig. Durch sie wird ganz zwingend offensichtlich, was beim Ent-Bündeln geschieht.
- Aus der ent-bündelten Zehnermenge können wir nun problemlos die noch fehlenden 2 herauslösen.
Und noch eine Hürde gibt es:
Wie sollen Kinder sich die 6 vorstellen, die wegkommen sollen?
Die Zehnergrenze erlaubt kein einfaches Abstreichen, das ja auch nur eine Form des Zurückzählens wäre und damit ohnehin für ein tieferes Verständnis des Stellenwertübergangs nicht taugt.
Hier hilft uns das Bild eines zu füllenden Tresors.
Die konkrete Vorgehensweise des Minusrechnens über den Zehner
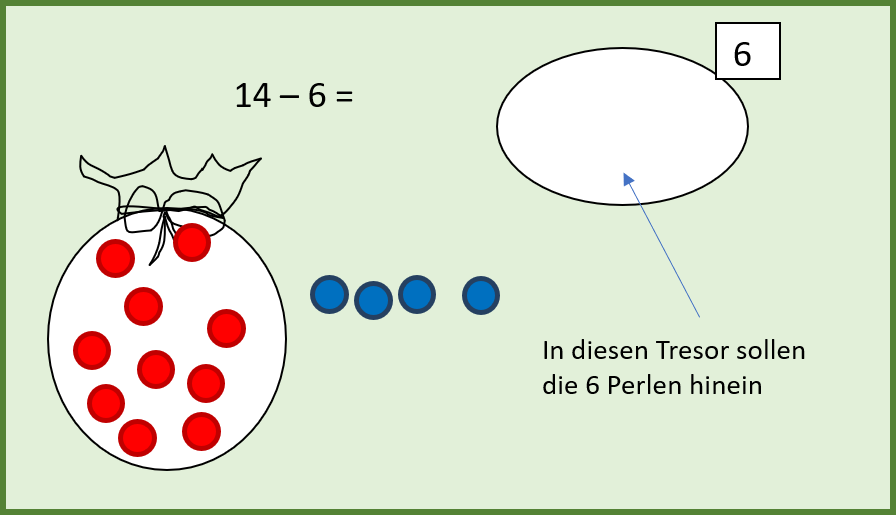
Hier das Ausgangsbild mit konkretem Material:
Ein Zehnersack mit roten Perlen, vier einzelne blaue Perlen.
Der Tresor soll mit 6 Perlen gefüllt werden, entsprechend ist die Mengenschleife beschildert.
An der Tafel kann das Bild durch einen Zehnersack, befestigt mit einem Magneten, und vier magnetische Wendeplättchen dargestellt werden.
Erster Schritt:
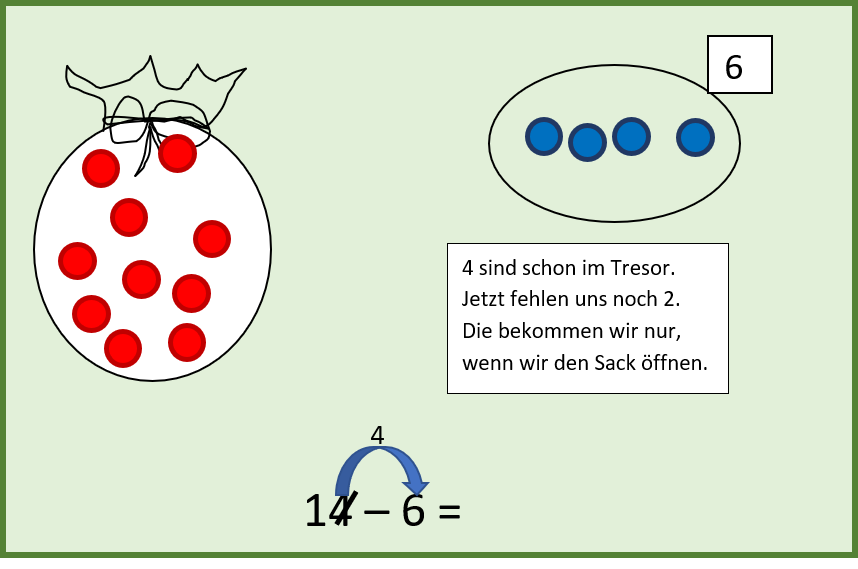
Die 4 einzelnen Perlen kommen in den Tresor. Die 4 in der Rechnung wird durchgestrichen, sie ist ja nicht mehr da und ein Pfeil zeigt an, wo die 4 Perlen hingekommen sind: Mit ihnen wurde begonnen, die 6 aufzufüllen.
Zweiter Schritt: Wir öffnen den Zehnersack und leeren ihn aus.
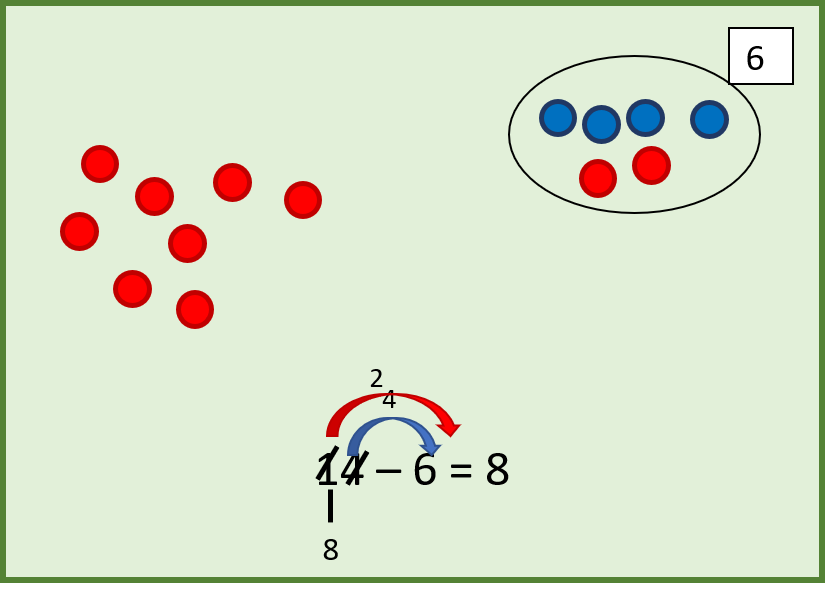
Bei der Demonstration an der Tafel wird der Zehnersack beim Öffnen durch 10 Magnet-Wendeplättchen ersetzt. Die Kinder hingegen öffnen die Zehnersäckchen „in echt“.
Nun können die fehlenden 2 Perlen in den Tresor gelegt werden.
In der Rechnung sieht das so aus:
Der Zehner ist durchgestrichen, er wurde ja ent-bündelt. Ein zweiter Pfeil deutet zur 6 hinüber, die nun vollkommen aufgefüllt ist.
Unter dem Zehner zeigt ein Ast, wie viele noch übrig sind: 8
An der Rechnung ist alles abzulesen:
Die 6 wurde in zwei Schritten von der 14 abgezogen: erst die 4 einzelnen (blaue Perlen), dann nach dem Ent-Bündeln die 2 noch fehlenden (rote Perlen).

Arbeit auf dem Blatt und im Heft mit Papiersäckchen
Nach den ersten Übungen mit echten Säckchen soll nun bald der ganze Vorgang im Heft festgehalten werden.
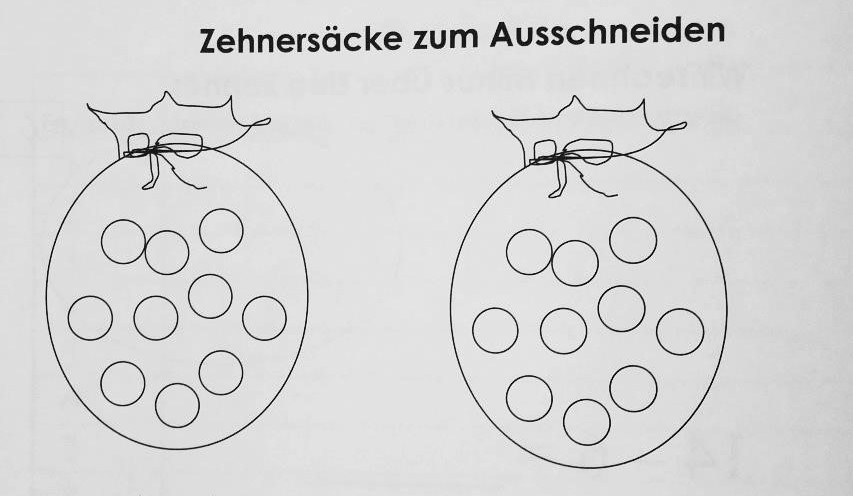
Dazu brauchen wir Papiersäckchen, in die zehn Perlen hineingemalt sind.
Die werden zunächst nur lose auf Arbeitsblatt oder Heft aufgelegt, denn sie müssen ja im weiteren Verlauf geöffnet werden.
Auch beim Minusrechnen kommt nun eine emotionale Komponente ins Spiel.
Beim Öffnen der Papiersäcke hilft nämlich das Krokodil Schnappi.

Mit Schnappi haben auch die Kolleginnen ihren Spaß, wie man sieht!
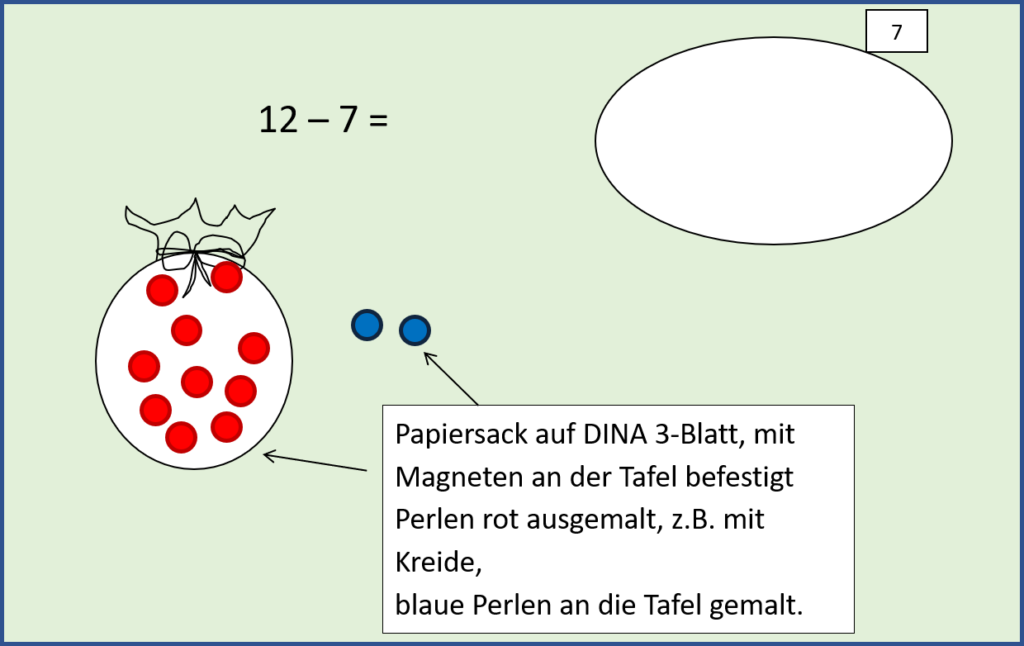
Erster Schritt:
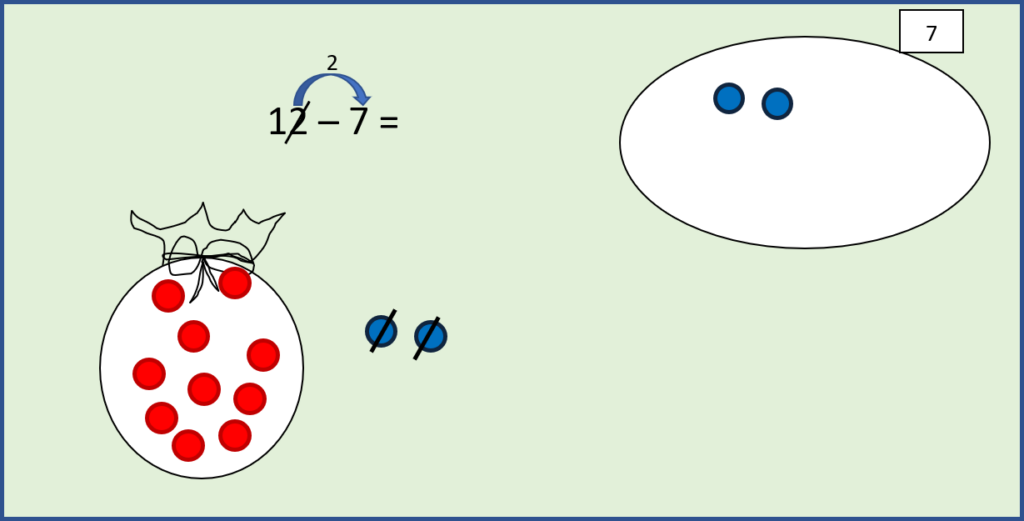
Die blauen Perlen werden durchgestrichen und in den Tresor gemalt, an der Rechnung wird mit einem Pfeil notiert, was gemacht wurde.
Zweiter Schritt:
Jetzt muss der Zehnersack geöffnet werden. Denn aus dem geschlossenen Zehnersack können keine Perlen genommen werden, das wäre systemwidrig.
Beim Öffnen des Sackes tritt nun das Krokodil Schnappi auf den Plan und während wir alle den Refrain des Schnappi-Liedes singen, wird der Sack „geköpft“.
Je nach darstellerischer Freude kann das mit einem lauten Schrei verbunden werden – der Sack brüllt natürlich, wenn er geköpft wird. Aber das bleibt der Interpretation der jeweiligen Lehrkraft überlassen.
Mathematisch betrachtet, wäre das Aufschneiden des Sackes natürlich auch ohne Schnappi möglich, würde aber bei den Kindern weit weniger Eindruck hinterlassen und gerade dieser Eindruck und das emotionale Sich-Einlassen auf die Situation bewirken weit größere Lernchancen und auch Lernfreude.

Schni-schna-schnappi, schnappi schnappi schnapp,
Schni-schna-schnappi, schnappi schnappi schnapp.
Nach dem „Köpfen“ des Sackes wird dieser mit der Öffnung nach unten wieder an der Tafel befestigt und nun können die noch fehlenden 5 Perlen abgestrichen und in den Tresor gemalt werden.
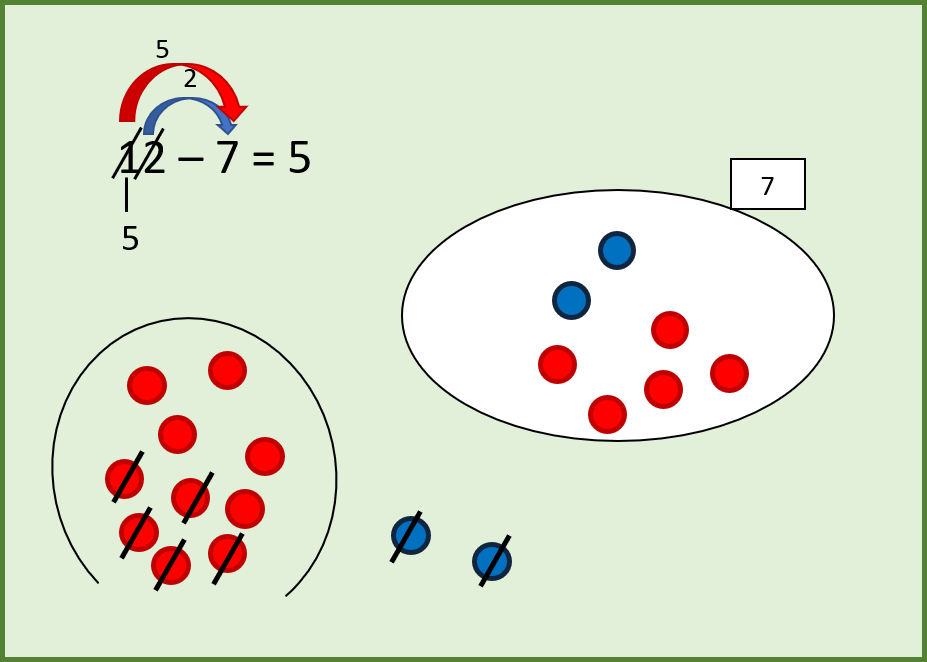
In der Rechnung wird der Zehner durchgestrichen, ein zweiter Pfeil zeigt uns, dass die 7 mit den noch fehlenden 5 Perlen aufgefüllt wurde, ein Ast zeigt, dass noch 5 Perlen übrig sind.
Arbeit auf dem Blatt und im Heft
Die Kinder machen nun das Gleiche, was an der Tafel gezeigt wurde, zuerst auf Arbeitsblättern, auf denen die Aufgabe und der Tresor vorgegeben sind, dann ins Heft.
Es gibt Papiersäckchen, die gelegt, aufgeschnitten und dann eingeklebt werden können, genauso, wie es an der Tafel gezeigt wurde.
Nun hast du viele Möglichkeiten gesehen, handlungsorientiert und schrittweise an das Minusrechnen heranzugehen. Und vielleicht glaubst du, ich übertreibe, aber bisher habe ich nur erlebt, dass alle meine Schüler es lernten, richtig plus und minus über die Zehnergrenzen zu rechnen und gerade das Minusrechnen mit Schnappi war immer ein großer Hit.
Ist das nicht toll, eine Möglichkeit zu haben, die die Kinder richtig begeistert für so ein „eigentlich“ unbeliebtes Thema?
Probier’s aus und du wirst sehen, es klappt!
